More results...


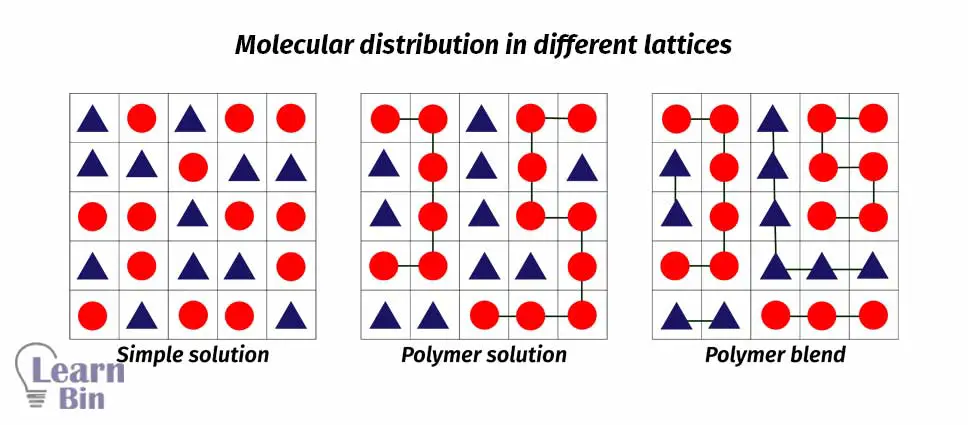
The Flory Huggins mean-field theory introduces entropic and enthalpic contributions of mixing of two different chemical species. This theory considers interactions between molecules are due to the interaction of a given molecule and an average interaction force of all the other molecules in the system. The mixture is imagined as a lattice and all the molecules have occupied lattice sites.
In Flory Huggins theory, there are two assumptions are considered,
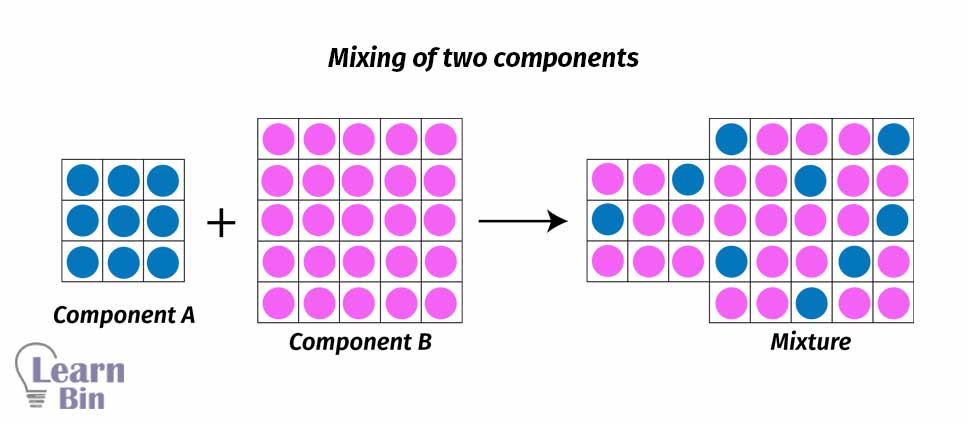
When mixing two species of A and B, if the volume of species A is VA and the volume of species B is VB, the total volume after mixing is given by VA+VB. It considers the components are randomly mixed to fill the entire lattice according to the Flory Huggins theory. The volume fractions of both components A and B are given by,
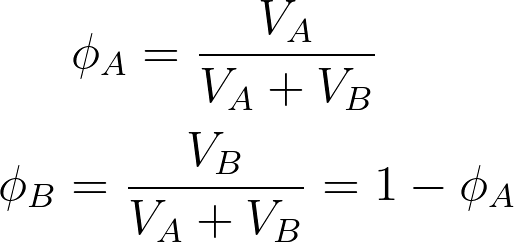
The lattice site is defined as the position of a molecule. The volume of the lattice site is similar to the volume of a single molecule. Here it is assumed that all the simple molecules have the same volume. One simple molecule occupies a single lattice site while large molecules such as polymers occupy multiple connected lattice sites. Generally, a repeating unit of a polymer occupies a single lattice site. If the volume of a single lattice site is V0, the volume of components A and B can be represented as,
VA = NAV0
VB = NBV0
NA and NB are the number of lattice sites occupied by each molecule. The total number of lattice sites are given by,
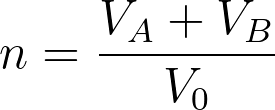
Number of lattice sites occupied by species A
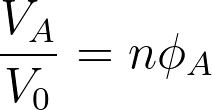
Number of lattice sites occupied by species B
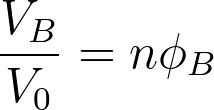
| Mixture | NA | NB |
| Regular solution | 1 | 1 |
| Polymer solution | Degree of polymerization | 1 |
| Polymer blend | Degree of polymerization | Degree of polymerization |
Regular Solutions:
Mixtures of low molar mass species with NA = NB = 1
Polymer Solutions:
Mixtures of macromolecule (N>> 1) with the low molar mass solvent (N=1)
Polymer Blends:
Mixtures of macromolecules of different chemical species having NA >>1 and NB>>1
Entropy is a measure of disorderness. By definition
S = k ln Ω
In a homogeneous mixture of A and B, each molecule has
ΩAB = n
Possible states, where n is the total number of lattice sites of the combined system
ΩA = n ΦA
ΩB = n ΦB
For a single molecule of species, A, the entropy change on mixing is
ΔSA = k ln ΩAB - k ln ΩA
ΔSA = k ln (ΩAB/ ΩA)
Where, ΩAB = n and ΩA = n ΦA,
ΔSA = k ln (n/ n ΦA)
ΔSA = k ln (1/ ΦA)
ΔSA = - k ln (ΦA)
ΔSB = - k ln (ΦB)
Since volume fraction is always < 1, the Entropy change of mixing is always positive
ΔS= - k ln (Φ) > 0
To calculate the total entropy of mixing, the entropy contributions from each molecule in the system are summed.
ΔS mix = nA ΔSA + nB ΔSB
ΔS mix = - k (nA ΦA + nB ΦB)
Where nA and nB are the numbers of molecules per species A and B.
nA = (n ΦA)/ NA
nB = (n ΦB)/ NB
For a mixture of two polymers A and B; Entropy of mixing per lattice site is given by,
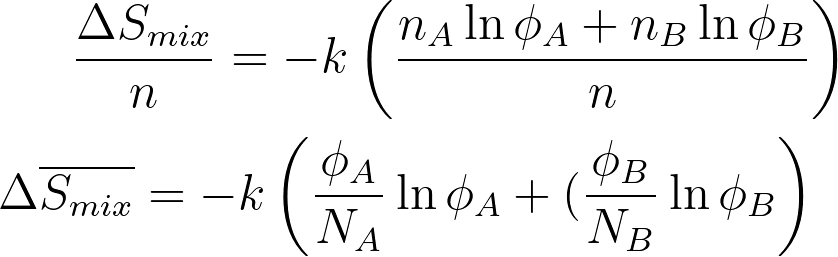
Gibbs free energy (ΔG) is defined under constant temperature and pressure. When it is defined under constant temperature and volume, it is called Helmholtz free energy (ΔF). Under constant pressure and temperature, the internal energy is called enthalpy (ΔH).
ΔG = ΔH - T ΔS
ΔF = ΔU - T ΔS
Where,
F-H model considers the constant volume condition. Thus, the energy of interactions will be explained in terms of Helmholtz's free energy of mixing. There are some assumptions considered,
Interactions can be explained in terms of pairwise interaction energies between adjacent lattice sites. In a binary mixture following interactions are occurred.
The probability of finding adjacent cells filled by components A and B is given by assuming the probability that a given cell is occupied by particular species is equal to the volume fraction of that species. Therefore, average pairwise interactions of a monomer species A with its neighbor can be given
UA = uAA ΦA + uAB ΦB
Likewise,
UB = uBB ΦB + uAB ΦA
Each lattice site of a regular lattice has “z” nearest neighbors (z-coordination number of the lattice)
Therefore, the average interaction energy of an A monomer with all of its z neighbors is zHA. The average energy per monomer is half of this energy (zHA/2). The total number of monomers of species A and B are n ΦA and n ΦB respectively. Therefore, the total interaction energy of the mixture is given by,
U2 = zn/2 [HA ΦA + HA ΦA]
U2 = zn/2 {[ ΦA (uAA ΦA + uAB ΦB)]+ [ΦB (uBB ΦB + uAB ΦA)]}
U2 = zn/2 (uAA ΦA2+ uBB ΦB2+ 2uAB ΦAΦB)
Energy before mixing
Interaction energy per site in a pure A component before mixing is (zuAA /2) Because before mixing, A molecules are surrounded by only A molecules. The total number of monomers of species A and B are nΦA and nΦB respectively. Therefore, the total energy of species A and B before mixing is
U1 = zn/2 (uAA ΦA + uBB ΦB)
Therefore, the enthalpy change of mixing is
ΔU = H2 - H1
ΔU = zn/2 (uAA ΦA2+ uBB ΦB2+ 2uAB ΦAΦB) - zn/2 (uAA ΦA + uBB ΦB)
ΔU = zn/2 (uAA ΦA2- uAA ΦA + uBB ΦB2 - uBB ΦB + 2uAB ΦAΦB)
ΔU = zn/2 (uAA ΦA (ΦA - 1) + uBB ΦB (ΦB -1) + 2uAB ΦAΦB)
Where, ΦB = 1 – ΦA
ΔU = zn/2 [uAA ΦA (ΦA - 1) + uBB (1- ΦA) (1 - ΦA -1) + 2uAB ΦA(1-ΦA)]
ΔU = zn/2 [uAA ΦA (ΦA - 1) + uBB (1- ΦA) (1 - ΦA -1) + 2uAB ΦA(1-ΦA)]
ΔU = zn/2 [uAA ΦA (ΦA - 1) - uBB ΦA (1 - ΦA) + 2uAB ΦA(1-ΦA)]
ΔU = zn/2 (ΦA ΦB) (uAB -uAA - uBB)
Helmholtz free energy for mixing per lattice site,
ΔU̅ = ΔU/n
ΔU̅ = z/2 (ΦA ΦB) (uAB -uAA - uBB)
χ is a dimensionless measure of the differences in the strength of pairwise interaction energies between species in a mixture. χ value depends on the temperature.
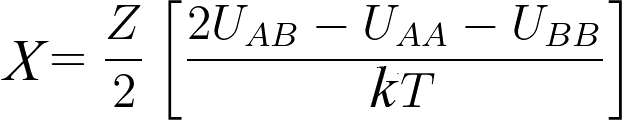
Where,
Helmholtz free energy for mixing per lattice site,
ΔF̅ mix = ΔU̅ mix - T ΔS̅ mix
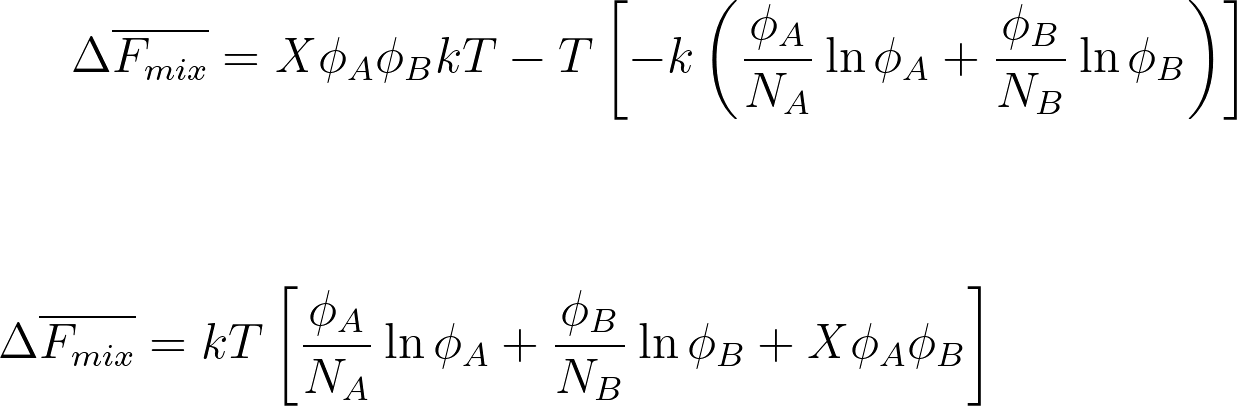
| χ value | Solubility |
| + | Not favorable for mixing |
| - | Favorable for mixing always |
| 0 | Favorable for mixing. Ideal situation |

The cover image was designed by using an image by frakir, licensed under CC BY-SA 3.0, via Wikimedia Commons