More results...

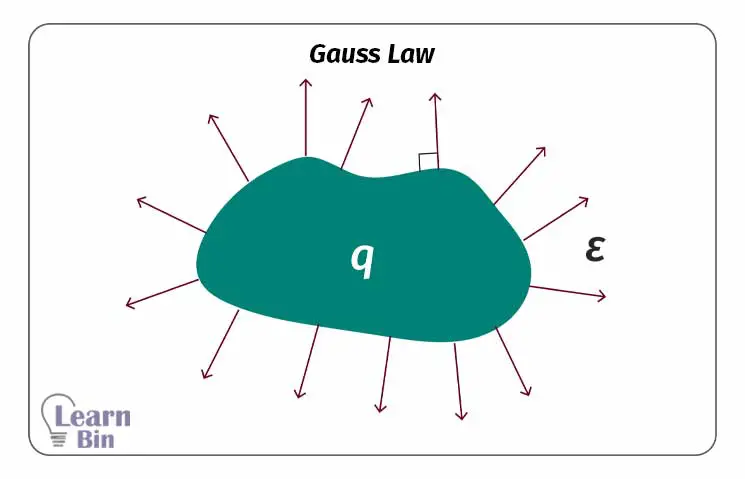
Gauss law states that the number of electric field lines perpendicular to a given closed surface (Electrical flux) is equal to the ratio of the charge contained on that closed surface to the permittivity of the medium.
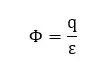
Where,
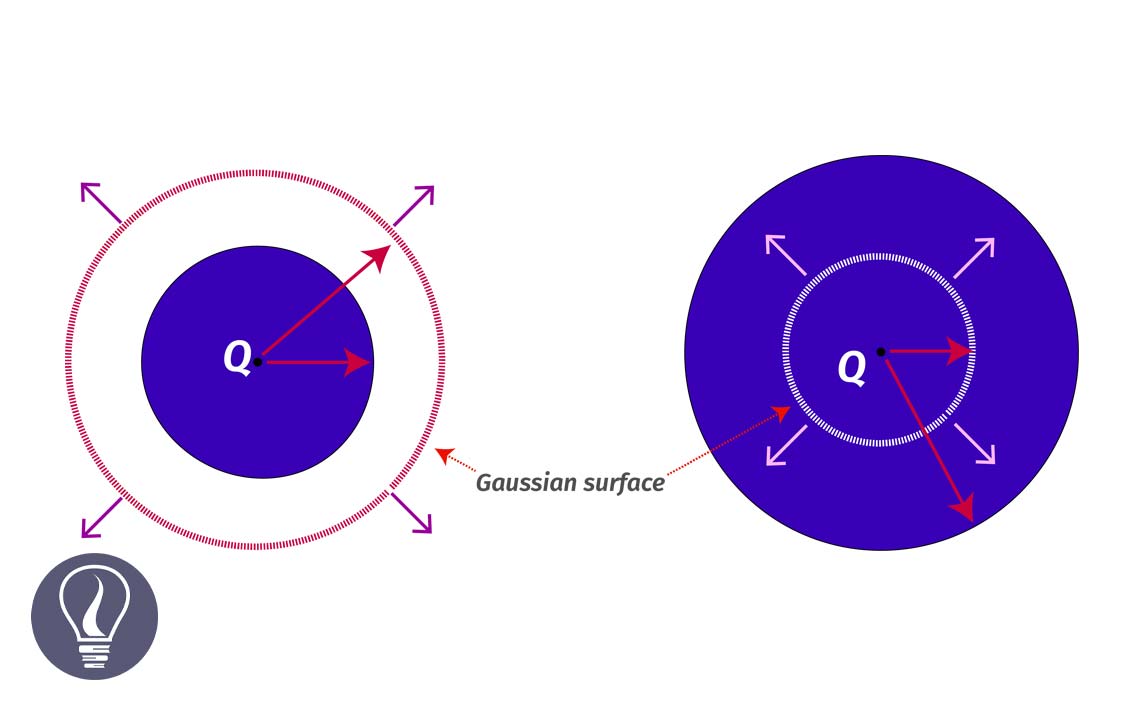
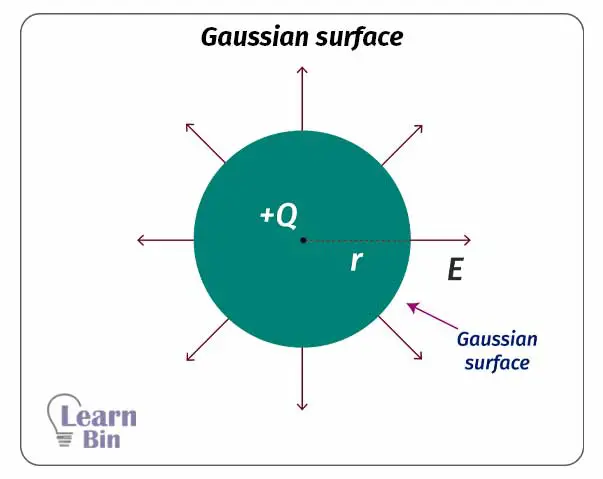
Let's consider an imaginary surface that surrounds a pointed charge. This surface is known as a Gaussian surface. If the radius of the sphere is r, the charge of the pointed charge is q, and the electric field intensity of the Gaussian surface is E, the Gaussian equation can be derived as follows.
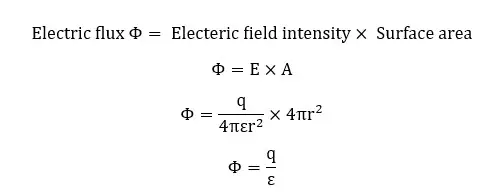
Let's consider a conductor ball with a radius of r and a charge of +q. To calculate the electric field intensity, we can consider three points that are inside the sphere, on the sphere, and outside the sphere.
We can consider a Gaussian surface with a radius of "a", which is less than the radius of the sphere. (Where a < r) According to Faraday's principle, there is no charge inside a conductor.
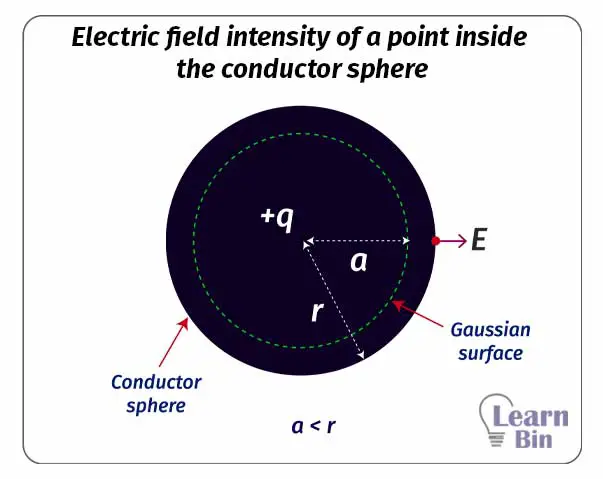
Therefore, the electric field intensity of a Gaussian surface that is inside a conductor is zero. Mathematically,
The electric flux through the Gaussian surface,
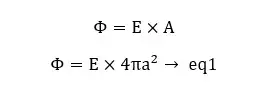
From Gauss law,
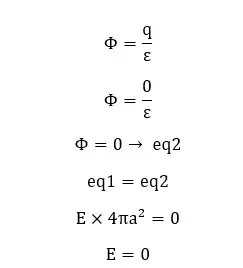
Let's consider a point on the conductor sphere. We can consider a Gaussian surface that has a similar radius to the conductor sphere. According to Faraday's principle, all the charge of a conductor exists on the outer surface. Therefore, there is an electric field intensity on the surface.

Mathematically,
The electric flux through the Gaussian surface,
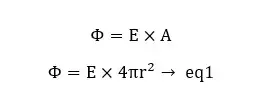
From Gauss law,
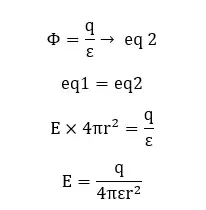
Let’s consider a point that is outside of the sphere. We can consider a Gaussian surface that has a radius (R) higher than the radius of the sphere (r). With the increase of the radius, the electric field intensity is rapidly decreasing.
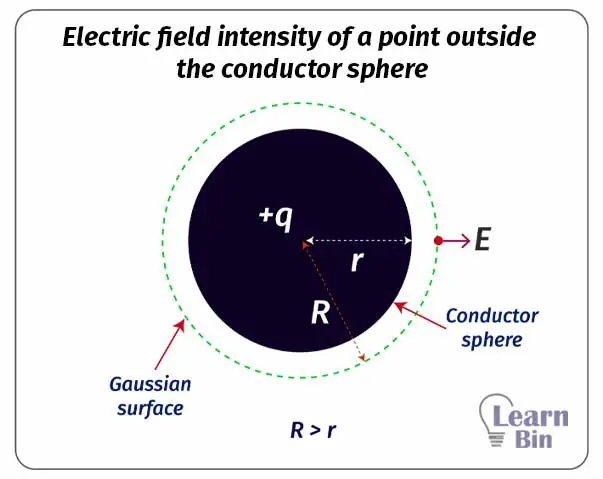
Mathematically,
The electric flux through the Gaussian surface,
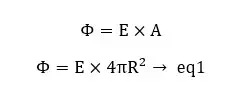
From Gauss law,
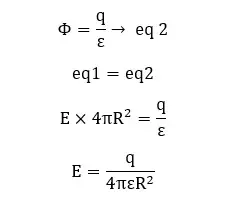
The change of electric field intensity from the center of the sphere can be shown as follows.
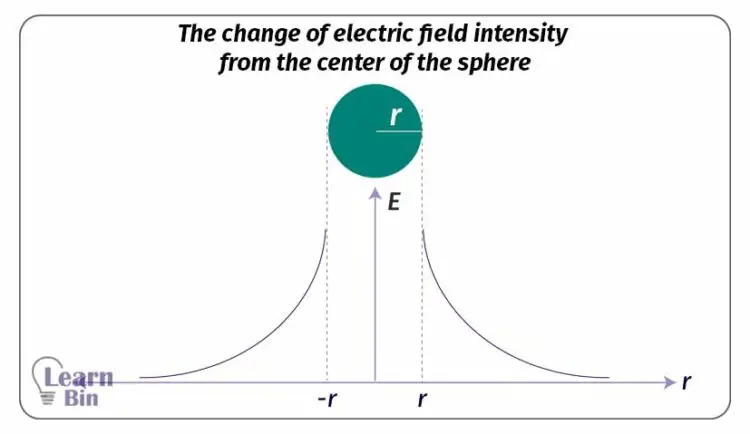
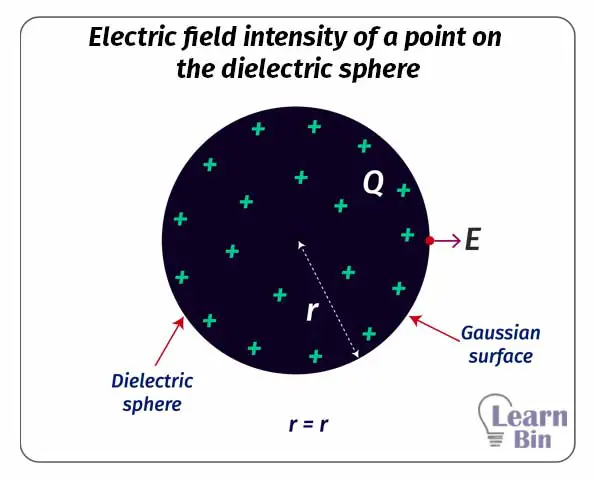
In dielectric materials, the charge is spread out through the entire volume of the material. If we consider a dielectric sphere with a radius of r and a charge of q, we can calculate the electric field intensity inside the sphere, on the sphere, and outside the sphere.
Let's consider a Gaussian sphere with a radius of "a” that is smaller than the radius of the dielectric sphere. Unlike in conductor spheres, the charge is distributed through the sphere in dielectric material. Therefore, first, we should calculate the charge that is covered by the Gaussian surface.
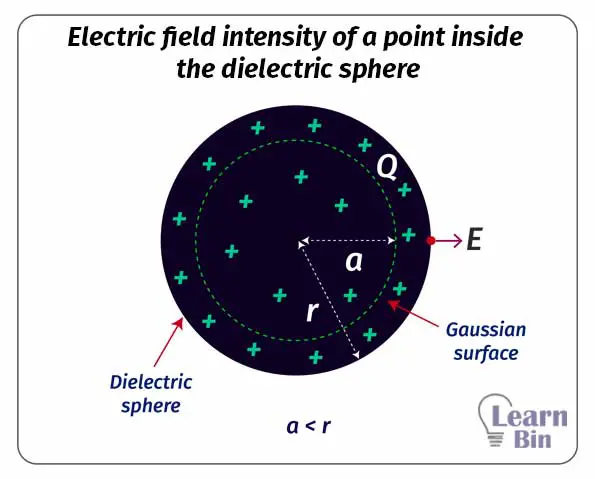

The electric flux through the Gaussian surface,
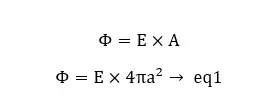
From Gauss law,
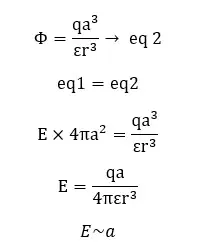
Here, the dielectric sphere is considered a closed Gaussian sphere. The radius of the Gaussian surface is similar to the radius of the dielectric sphere (a = r). Mathematically,
The electric flux through the Gaussian surface,
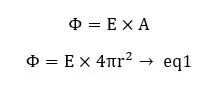
From Gauss law
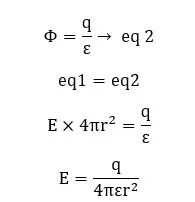
Let’s consider a point that is outside of the sphere. We can consider a Gaussian surface that has a radius (R) higher than the radius of the sphere (r). With the increase of the radius, the electric field intensity is rapidly decreasing. Mathematically,
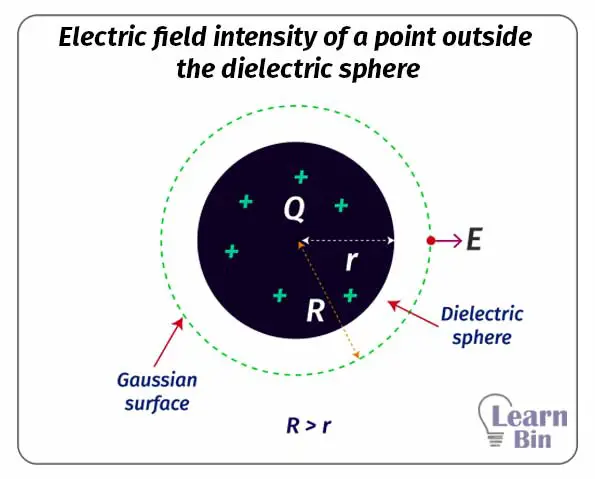
The electric flux through the Gaussian surface,
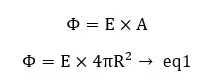
From Gauss law
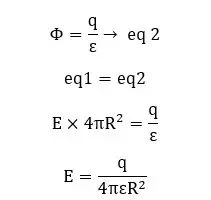
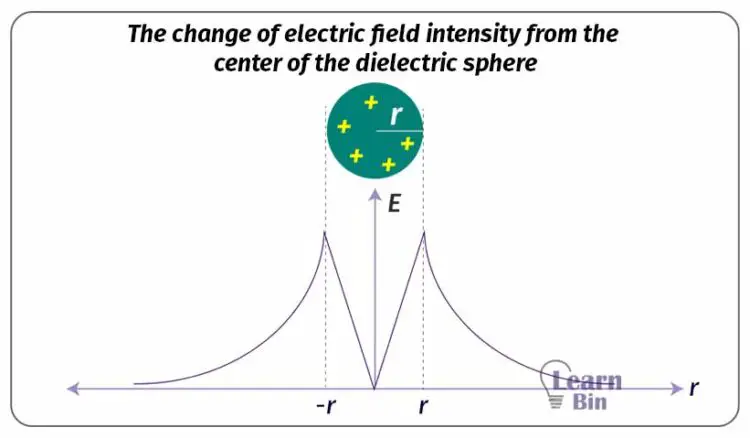
The change of electric field intensity from the center of the sphere can be shown as follows.
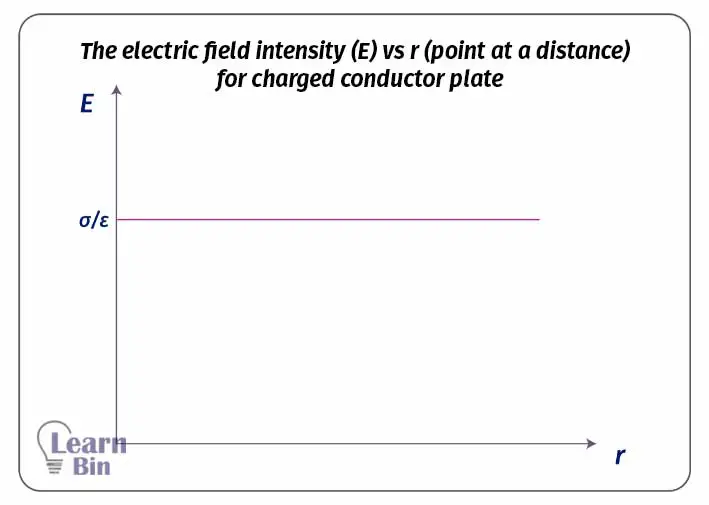
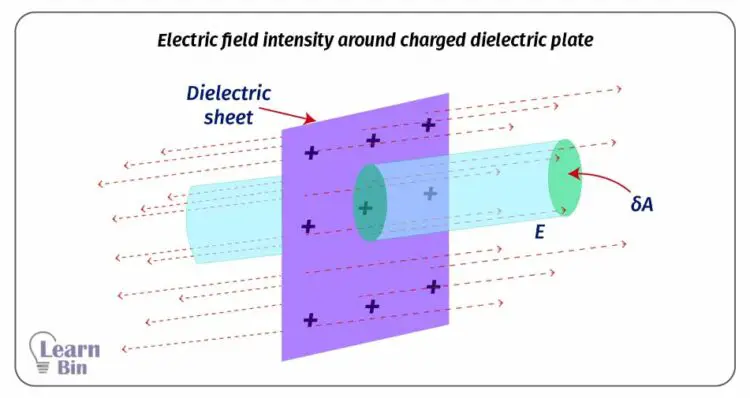
Consider a thin plate of conductors with a surface charge density of σ. Electric field lines exist only on one side of a conducting plate. Let's find the Electric field intensity of a point that is at a distance of "r" from the plate. If the electric field intensity is E, at a point at a distance r from the plate, consider a circular area (δA) parallel to the plate around that point. Here, this area is considered as the Gaussian surface.
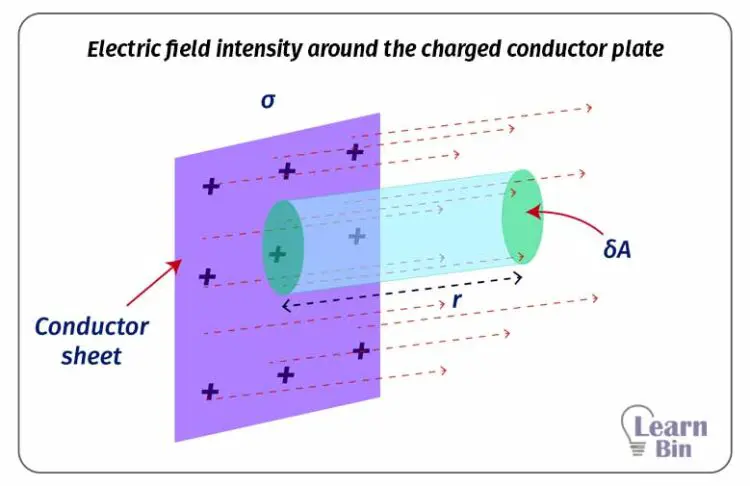

The electric flux through the Gaussian surface,
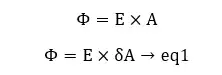
From Gauss law
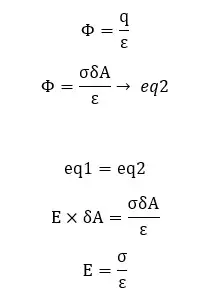
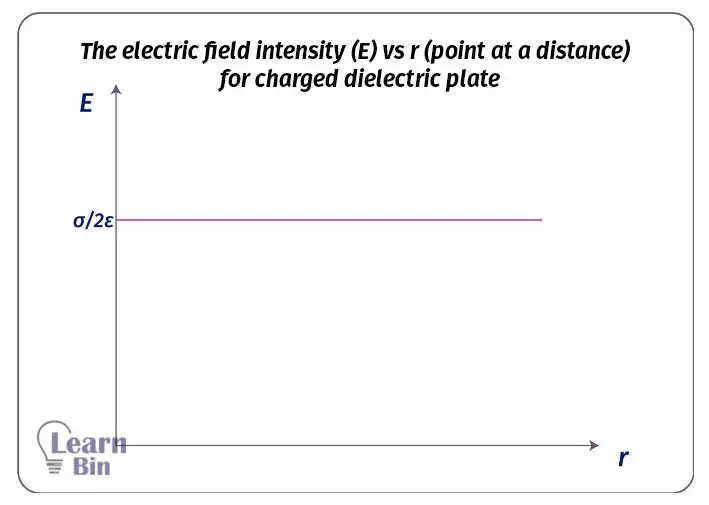
Consider a thin plate of dielectric material with a surface charge density of σ. Electric field lines exist on both sides of the dielectric plate. Let's find the Electric field intensity of a point that is at a distance of "r" from the plate. If the electric field intensity is E, at a point at a distance r from the plate, consider a circular area (δA) parallel to the plate around that point.
Here, this area is considered as the Gaussian surface. Since there is flux on both sides of the plate, the surface area of the Gaussian surface would be 2δA.

The electric flux through the Gaussian surface,
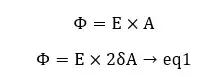
From gauss’ law,
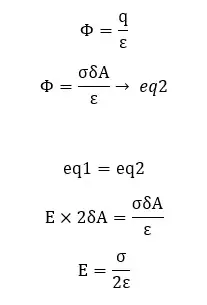
Let's determine the intensity at a point near the wire when a static electric charge rests on a straight, thin, uniform length of wire. If the linear charge density of the wire is λ and the length of the wire is l, consider a point near the wire at a distance of r. The electric field intensity of that point is E. We can consider a cylindrical Gaussian surface that is surrounding the wire.
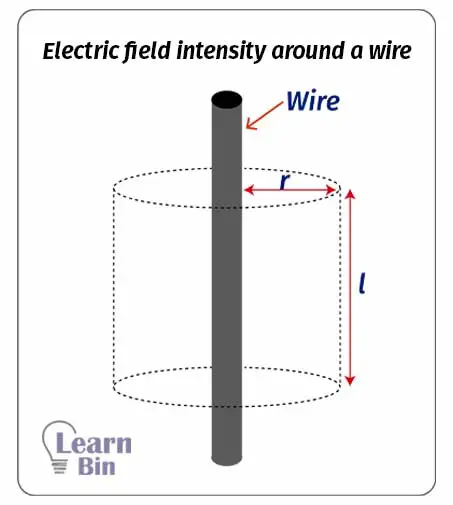

The electric flux through the Gaussian surface,
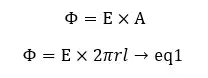
From gauss’ law,
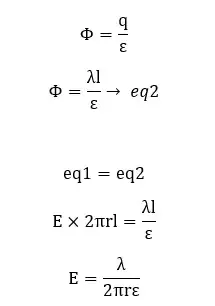
Consider a charge conductor with a surface charge density of σ. To find the electric field intensity at a point near the conductor, let's consider a small circular area that is centered by the point.
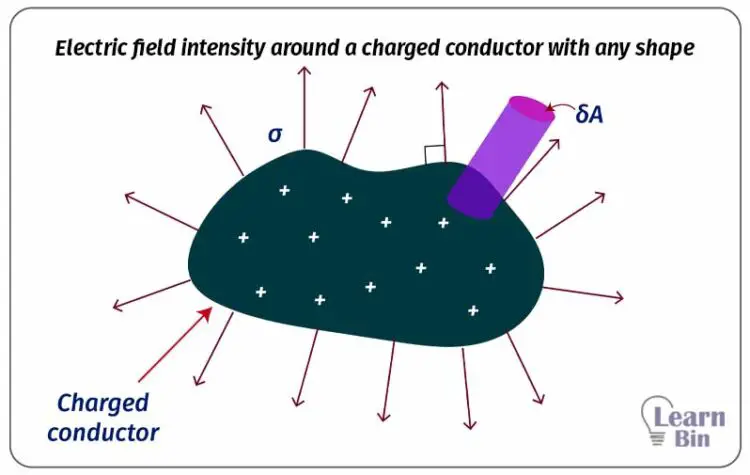

The electric flux through the Gaussian surface,
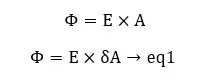
From gauss’ law,
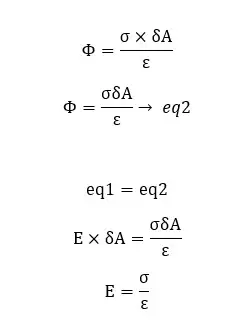
To calculate the force acting on the charge on a conductor, we can consider two points, one is just inside the conductor and the other one is just outside the conductor.
Let's take these points as X and Y. Y is inside the conductor and X is outside the conductor. To find the electric field intensity acts on X and Y, consider a Gaussian surface with the area of δA, that is on the surface of the conductor.
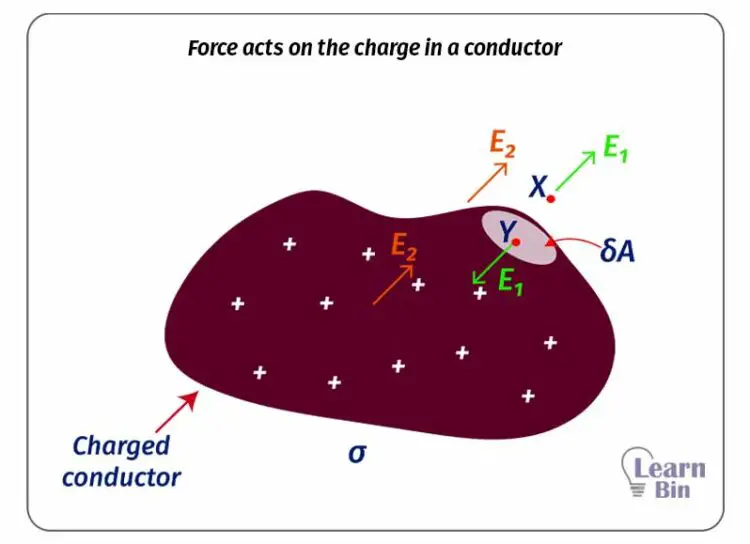
For point Y,
An electric field intensity acts on the point a due to the charge of the Gaussian surface. Another electric field intensity acts on point Y due to the remaining charge in the conductor. These two intensities act in opposite directions on point Y. Since there is no charge inside a conductor there is no electric field intensity on point Y. Mathematically,
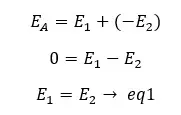
Where EA is the electric field intensity at point Y, E1 is the electric field intensity due to the charge of the Gaussian surface, and E2 is the electric field intensity due to the remaining charge in the conductor.
For point X,
As in point Y, electric field intensities act on point X, due to the charge of the Gaussian surface and the remaining charge of the conductor. But in point X, both intensities act in the same direction. And there is an electric field intensity on point X. (It is not zero)
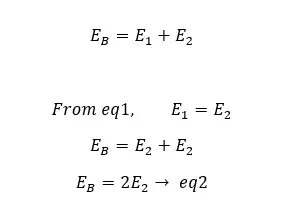
From Gauss law,
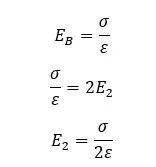
Where EB is the electric field intensity at point X, E1 is the electric field intensity due to the charge of the Gaussian surface, and E2 is the electric field intensity due to the remaining charge in the conductor.
According to the definition of electric field intensity, Electric field intensity is the force acting on a +1 C of charge.
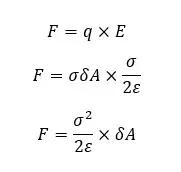

The cover image was designed using an image by Guy Vandegrift, licensed under CC0, via Wikimedia Commons