More results...


Generally, EDTA titrations are occurred to find the metal ions concentration in a solution. EDTA will be complex with metal ions with a 1:1 stoichiometric ratio. But in some cases, we add auxiliary complexing agents to the solution. The auxiliary complexing agent is a complexing agent which is also complexing with the metal ion, less strong than EDTA.
EDTA titrations are taken place at around pH = 10. At this pH level, the concentration of Hydroxyl ions (OH-) in the medium is very high. Some metal ions tend to form insoluble products with OH- ions. Therefore, the free metal ion concentration is reduced.
When we are titrating the above solution, only free metal ions will form a complex with EDTA. Some amount of metal ions have already been used and precipitated. So, we get a lower concentration of the metal ion than the actual concentration. Therefore, we should prevent metal ions from precipitating with OH- ions.
To prevent this, we add a new auxiliary complexing agent. Auxiliary complexing agents will complex with the metal ions more strongly than OH- ions and less strongly than EDTA.
When an auxiliary complexing agent is added to the solution, it will be complex with metal ions. If we consider that the metal ions form a complex with two ligands, the formation of the complex can be represented as a two-step process.
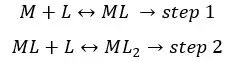
Formation constants for the above formation steps can be written as,
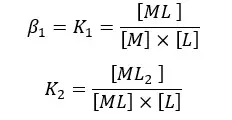
Overall formation of the complex,
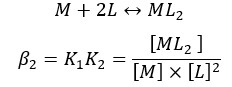
Where M is the metal ion and L is the ligand.
β is the cumulative formation constant or overall formation constant.
If the formation is a single-step process, β = K. If the formation is a multiple-step process, β can be found by multiplying the formation constants of each step.
After adding the auxiliary complexing agent, metal ions will form a complex with it. Therefore, there is only a fraction of free metal ions in the solution. If the formation is a two-step process, metal ions are in the form of M, ML, and ML2.
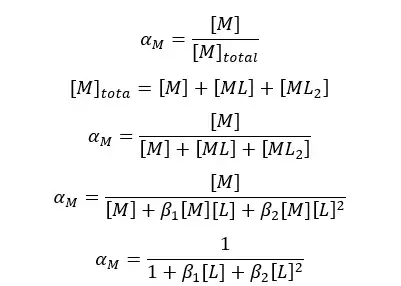
Where αM is the fraction of free metal ions in the solution.
This solution is titrated with EDTA. When adding EDTA, metal ions will be de-complexed with an auxiliary complexing agent and complexed with EDTA. The following equilibrium is written by considering the metal ion as a divalent ion.
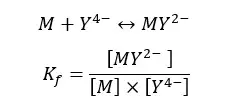
At pH = 10, we write the conditional formation constant of the [EDTA – metal ion] complex as follows.
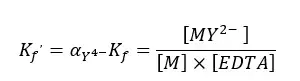
Where, αY4- is the fraction of EDTA and [EDTA] is the total concentration of EDTA. Since there is only a fraction of free metal ions in the solution, we need to modify the above conditional formation constant.
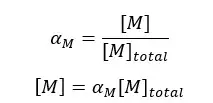
By substitution of the above values to the formation constant expression, we can obtain a new conditional formation constant.
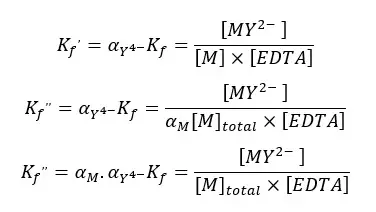
Question 01
Find the fraction of free Zn2+ ion concentration of a 0.1 M solution of Ammonia (NH3). Zn2+ ions and Ammonia form a 1:4 complex. At 30℃, the cumulative formation constants for [Zn - Ammonia] complexes are as follows.
| Complex | β |
| [Zn(NH3)]2+ | 1.51 × 102 |
| [Zn(NH3)2]2+ | 2.69 × 104 |
| [Zn(NH3)3]2+ | 5.49 × 106 |
| [Zn(NH3)4]2+ | 5.01 × 108 |
Solution
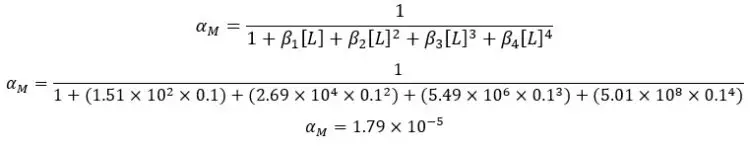
Question 02
Consider the titration of 50.0 mL of 0.001 M Zn2+ solution with 0.001M EDTA at pH 10.00. The solution has been added 0.10 M NH3 as an auxiliary complexing agent. If the equivalence point is at 50.0 mL, find pZn2+ at the equivalent point. At 25 ℃, αY4- = 0.3, αZn2+ = 1.79 × 10-5, the Formation constant of the [Zn- EDTA] complex is 3.16 × 1016.
Solution
At the equilibrium point, we consider that all the Zn2+ ions have complexed with EDTA. Therefore, the total mols of Zn2+ ions are equal to the total mols of the complex formed. The free Zn2+ ions come from the dissociation of the complex.
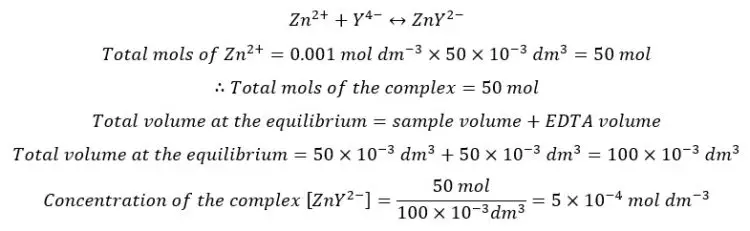
At the equilibrium, the formed complex is dissociated into free Zn2+ ions and free EDTA. If we take the dissociated Concentration of the complex as x, the concentration of each component at the equilibrium can be represented as follows.
| Zn2+ | Y4- | ZnY2- | |
| Initial concentration | - | - | 5 × 10-4 |
| Concentration at the equilibrium | x | x | 5 × 10-4 -x |
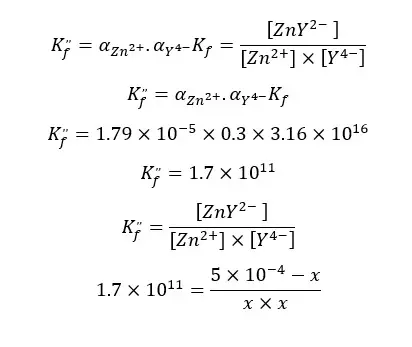
When compared to 5 × 10-4, x is negligible.
Therefore, (5 × 10-4 - x) is approximately equal to 5 × 10-4.
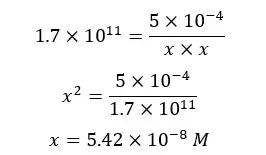
The above x value shows the total Zn2+ ions in the solution. But we need the concentration of free Zn2+ ions at the equilibrium point to calculate pZn2+ at the equilibrium point.
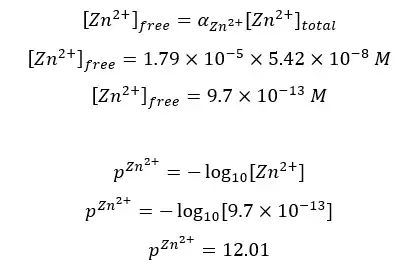

The cover image was designed using an image by André Künzelmann, licensed under CC BY-SA 3.0, via Wikimedia Commons