More results...


Ethylenediaminetetraacetic acid (EDTA) is the most widely used chelating agent in chelatometric titrations (complexometric titrations).
There are some organic agents that have the capability of forming stable and water-soluble complexes with metal ions. Those types of organic groups are called chelating agents. When the complex is formed it is called a chelate.
Because EDTA Is a good chelating agent, EDTA titrations are widely used for identifying unknown metal ion concentrations in solutions.
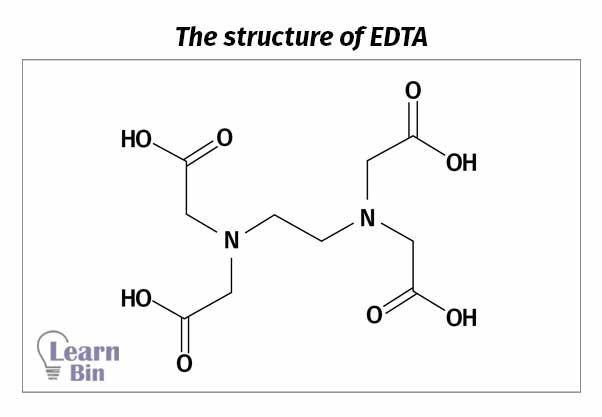
EDTA contains four carboxyl groups and two amino groups. Therefore, EDTA has six complexing groups.
Around pH 2, EDTA remains a tetra-protic acid. At this pH, four carboxylic groups have been protonated. We can represent EDTA as H4Y. (figure 1)
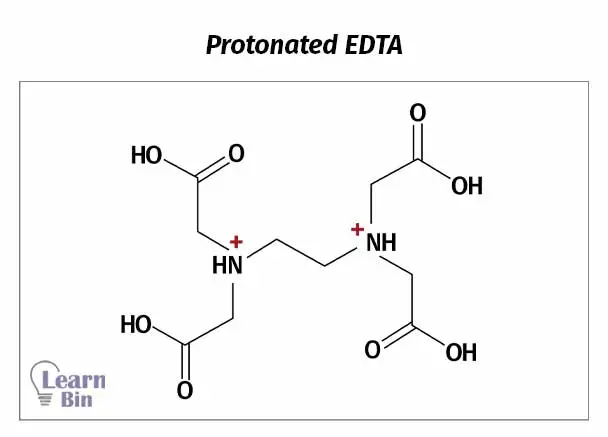
At very low pH values, nitrogen will also be protonated (figure 2). At this pH, EDTA has been diprotonated and it can be considered a hexa-protic acid (H6Y2+). But EDTA is almost never used in such conditions.
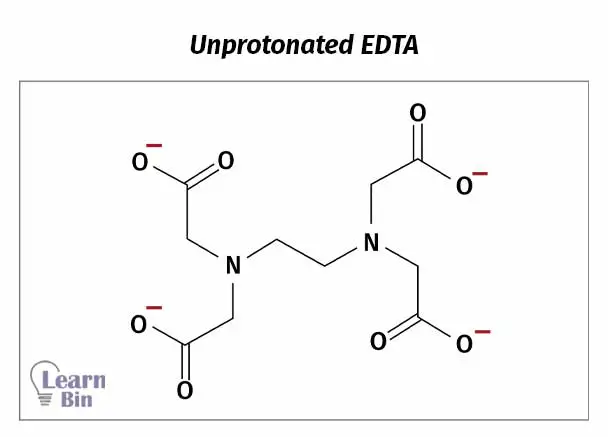
Unprotonated ligand (Y4-) forms complexes with metal ions. When complexation, protons (H+ ions) are replaced by metal ions.
We can write four Ka values for the stepwise dissociation of four protons in EDTA.

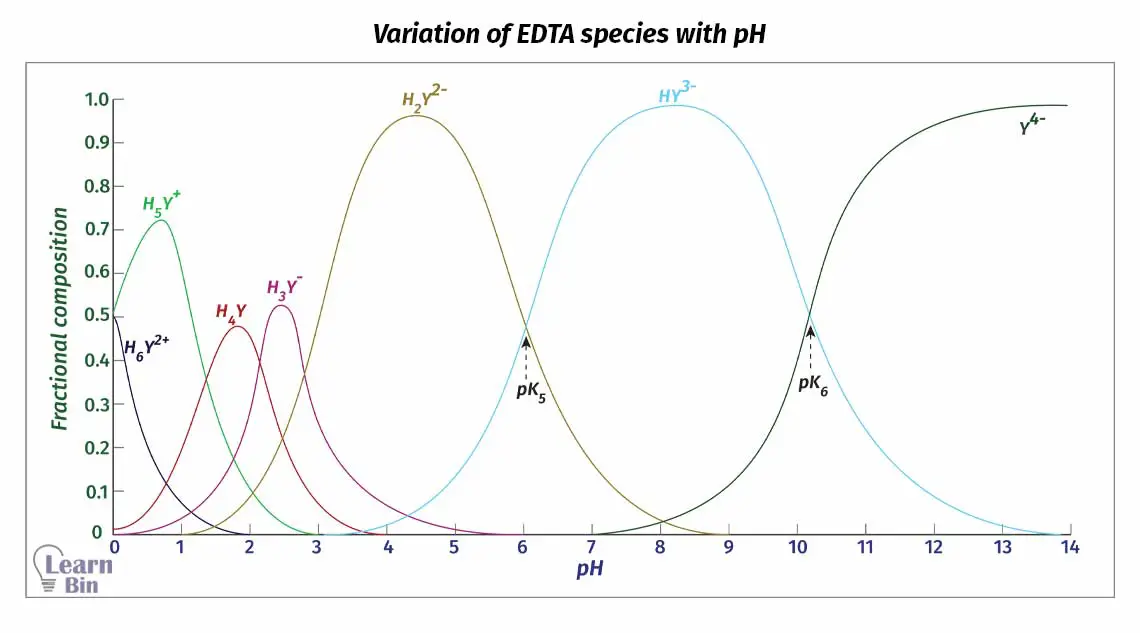
Dissociation of EDTA is directly affected by the pH of the medium. Therefore, the dominating species of the EDTA changes at different pH levels. H4Y has very low solubility in water.
So, the disodium salt (Na2H2Y·2H2O) of EDTA is used for titrations. Here two acid groups are neutralized. This salt will dissociate in the solution and predominantly give H2Y2− to the media around pH = 4 - 5.
Since the dissociation of EDTA is markedly affected by pH, the fraction of Y4- species changes at different pH levels. We can find the fraction of EDTA in the form of Y4- as follows.
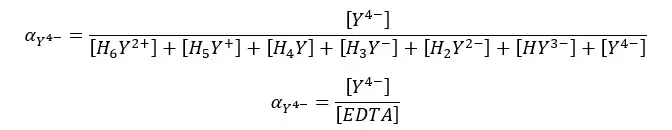
EDTA Titrations - Question 01
Find the fraction of all EDTA in the form of Y4- at pH = 6 and the formal concentration of 0.1 M. compositions of each species in the medium as follows.
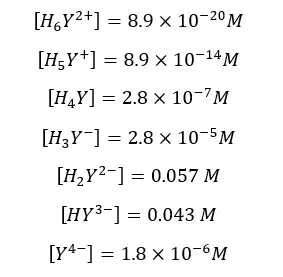
Solution
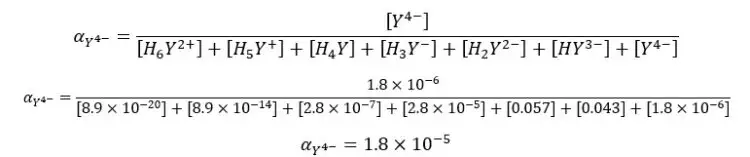
We can also find the fraction of EDTA in the form of Y4- using the equilibrium constants of each dissociation. Equilibrium reactions of EDTA that may occur in the medium, can be written as follows.
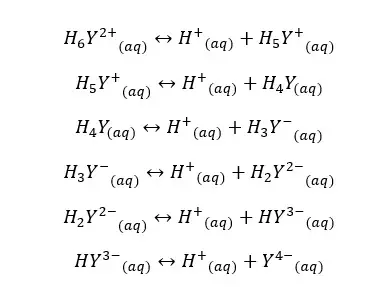
If the dissociation constants of the above equilibriums are K1, K2, K3, K4, K5, and K6, we can express the equilibrium constants and concentrations of each component as follows.
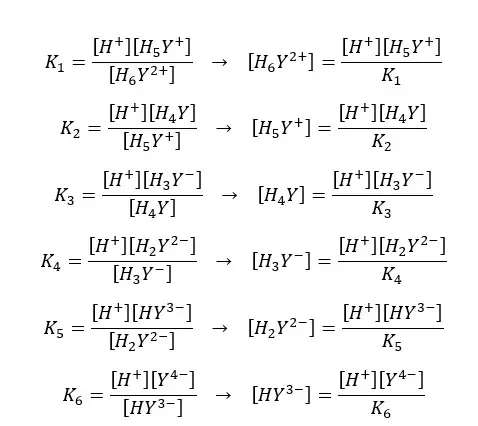
By substituting the above expressions to the equation, we can find the fraction of EDTA by using dissociation constants.
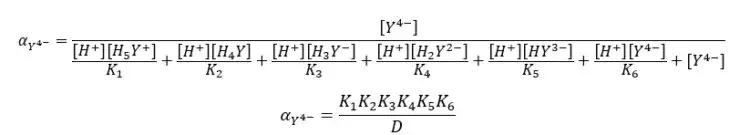
Where,
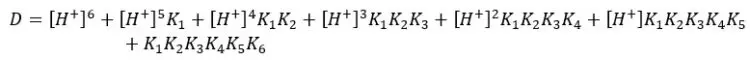
| pH | αY4- | pH | αY4- |
| 0 | 1.3 × 10-23 | 8 | 4.2 × 10-3 |
| 1 | 1.4 × 10-18 | 9 | 0.041 |
| 2 | 2.6 × 10-14 | 10 | 0.30 |
| 3 | 2.1 × 10-11 | 11 | 0.81 |
| 4 | 3.0 × 10-9 | 12 | 0.98 |
| 5 | 2.9 × 10-7 | 13 | 1.00 |
| 6 | 1.8 × 10-5 | 14 | 1.00 |
| 7 | 3.8 × 10-4 |
EDTA complexes with most of the metal ions and forms EDTA chelate. EDTA engulfs metal ions and forms six-coordinate species in many transition metal complexes. Let’s consider the formation of EDTA chelate with Mn+ metal ions.
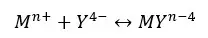
The formation constant for the above equilibrium,
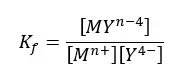
The formation constants of most EDTA - metal ion complexes are large. That means the equilibrium tends to form the complex. And the formation constants tend to be larger for more positively charged cations.
| Metal Ion | log(Kf ) | Metal Ion | log(Kf ) |
| Li+ | 2.95 | Zn2+ | 16.5 |
| Na+ | 1.86 | Fe3+ | 25.1 |
| K+ | 0.8 | Pb2+ | 18.0 |
| Mg2+ | 8.79 | Al3+ | 16.4 |
| Ca2+ | 10.65 | Ti3+ | 35.3 |
| Mn2+ | 13.89 | VO2+ | 18.7 |
| Fe2+ | 14.30 | Ag+ | 7.2 |
Here we have considered that only Y4- species of EDTA are reacting with metal ions to form the complex. It does not mean that metal ions are only complex with Y4- species. Any other forms of EDTA could be present in the solution. So, metal ions can be complex with any other species of EDTA.
In the general expression of formation constant, it has been described that the metal ion complexed with only Y4- ions. But most EDTA is not in Y4- form below 10.37 pH. At lower pH levels EDTA predominantly presents in HY3-, and H2Y2- forms.
Therefore, we should express the formation constant using the total concentration of EDTA instead of the concentration of Y4- ions. The modified formation constant is called the “Conditional formation constant” or “the effective formation constant”.
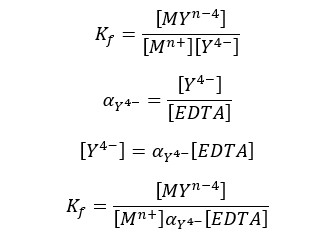
Where [EDTA] is the total concentration of all EDTA species not bound to a metal ion. We can rewrite the equation as follows.
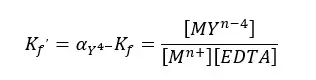
EDTA Titrations - Question 02
EDTA forms a strong 1:1 complex with Ca2+ ions. If the concentration of the formed complex is 0.1 M, find the concentration of free Ca2+ ions in the solution at pH = 10. The formation constant (Kf) of the CaY2- complex is 1 × 1010.65 mol-1 dm3. αY4- value at pH = 10 is 0.30.
Solution
EDTA and Ca2+ form the complex as follows.
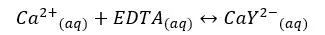
| Ca2+ | EDTA | CaY2- | |
| Initial concentration | 0 | 0 | 0.1 |
| Equilibrium concentration | x | x | 0.1 - x |
First, we should calculate the conditional formation constant for the above equilibrium.
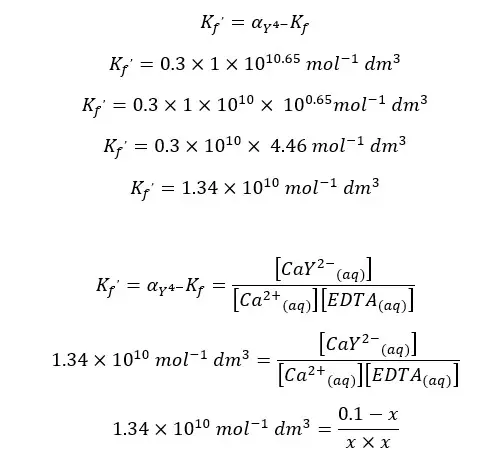
When compared to 0.1, x is very small. Therefore, 0.1 - x is approximately equal to 0.1. so, we can rewrite the above expression as follows.
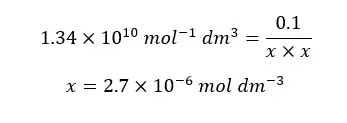

Harris, D.C. (1991) Quantitative Chemical Analysis. New York: Freeman.
Table 02: Donald R. Burgess (2004), NIST SRD 46. Critically Selected Stability Constants of Metal Complexes: Version 8.0 for Windows, National Institute of Standards and Technology, https://doi.org/10.18434/M32154 (Accessed 2023-03-19)
The cover image was created using an image by LHcheM, licensed under CC BY-SA 3.0, via Wikimedia Commons