More results...


In our previous article about acids and bases, there was a basic method of calculating pH and H+ concentrations. The answers you will get using that method, won’t be the most accurate answer. This article discusses a more accurate method to calculate the pH of acids and bases.
When considering the above problem and the answer in the previous article there is a better way of solving that. That answer is not a wrong answer, but it could be more accurate.
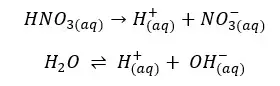
According to the above reactions, there are 3 types of ions present in the solution.
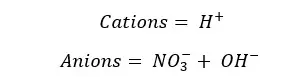
These are the ions present in the solution. So Total charge of the solution should be equal to the initial charge of the solution. In this case, it should be zero.
According to the charge balance,
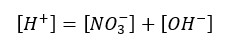
The solution gets H+ from both the dissociation of acid and the partial dissociation of the water. Because this strong acid fully dissociates, NO3- concentration should be equal to the initial concentration.
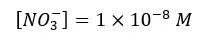
Even though at 250C Kw of water is 10-14, we cannot take [OH-] and [H+] from partial dissociation of water as 10-7M because water is not the only H+ source in the solution. According to ‘Le-Chatelier’s principle, an increase in the amount of products results in the backward biasing of an equilibrium. So [H+] and [OH-] from partial dissociation of water will be less than 10-7M.
Let's take total [H+] as ‘x’. Then [OH-] will be x – 1×10-8.
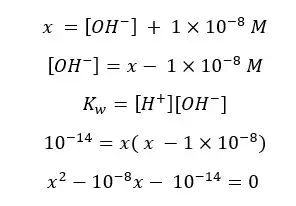
This equation can be solved using the quadratic formula.
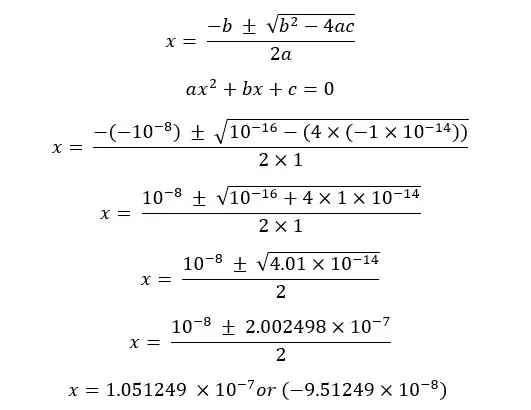
Concentration cannot be a negative value so

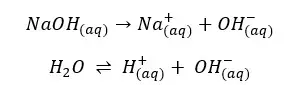
According to the above reactions, there are 3 types of ions present in the solution.
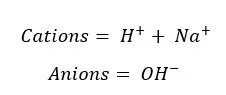
According to the charge balance,
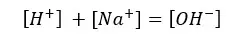
The solution gets OH- from both the dissociation of the base and the partial dissociation of the water. Because this strong base fully dissociates, Na+ concentration should be equal to the initial concentration.
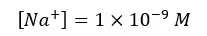
Let’s take total [H+] as ‘x’.
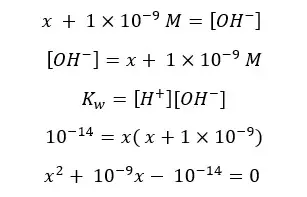
This equation can be solved using the quadratic formula.
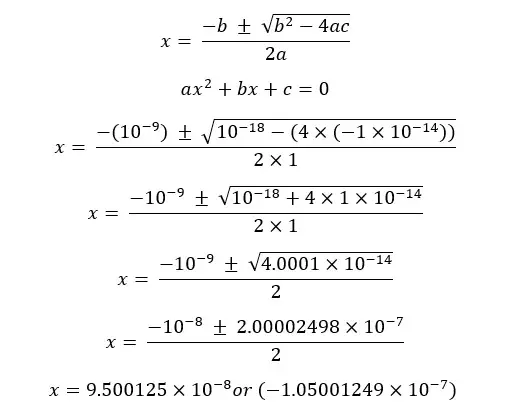
Concentration cannot be a negative value so

Find the pH of a CH3COOH (acetic acid) solution with an initial concentration of 0.01 mol dm-3 at 25℃. The dissociation constant (Ka) of CH3COOH at 25℃ is 1.8 ×10-5 mol dm-3 (pKa = 4.76). Also, find both [H+] from the dissociation of the acid and the dissociation of water separately.
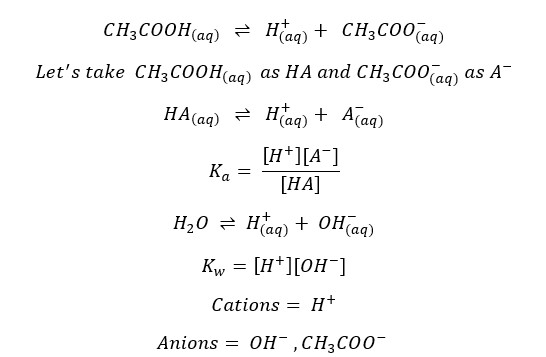
The charge should be balanced in the system
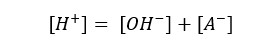
Lets take [H+] as x,
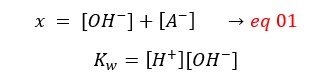
So,
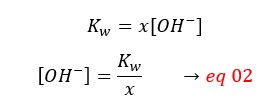
From eq 01 and 02,
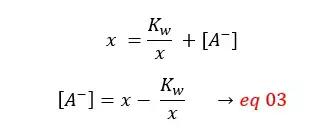
Because the initial concentration should be equal to the sum of products and reactants left,
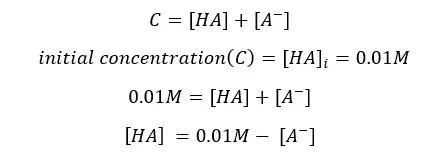
By substituting eq 03 for [A-],
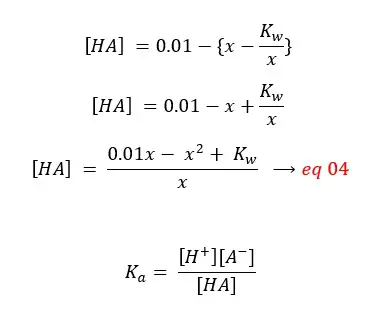
By substituting eq 04 for [HA], eq 03 for [A-],
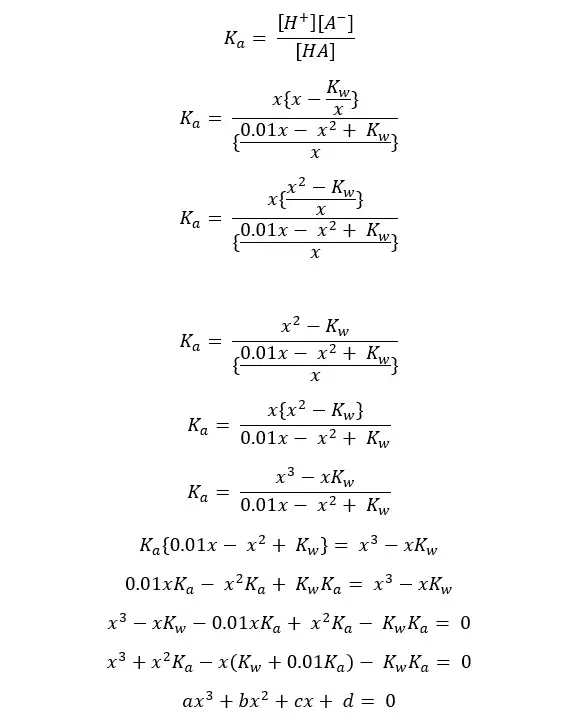
This type of equation is known as a 'cubic equation’. If you want the most accurate answer, you can get that by solving this.
In this case, we make some assumptions to simplify the above equation.
Assumption:
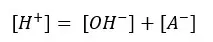
In the above situation, the solution gets OH- from the dissociation of water. When comparing that concentration with the concentration of A-, [OH-] will be a very small fraction of that.
Also, the acidic environment of the solution (extra H+ from the dissociation of the acid) discourages the dissociation of water because according to ‘Le Chatelier’s principle. (Because the solution has much greater [H+] from the acid. That will favor the backward reaction).
So,
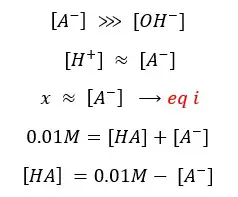
By substituting eq i for [A-],
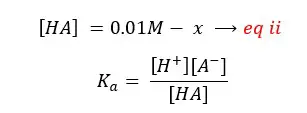
By substituting eq ii for [HA], eq i for [A-],
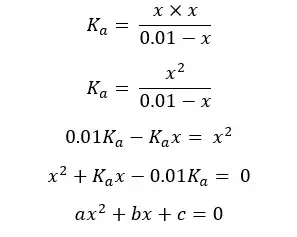
This equation can be solved using the quadratic formula.

Concentration cannot be a negative value so,
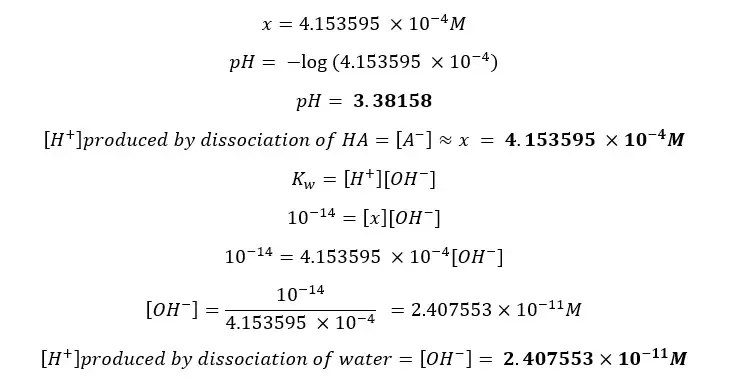
Find the pH of a CH3NH2 (Methylamine) solution with the initial concentration of 0.05 mol dm-3 at 25℃. The dissociation constant (Kb) of CH3NH2 at 25℃ is 4.4 ×10-4 mol dm-3 (pKb = 3.35). Also, find [H+] from the dissociation of water.
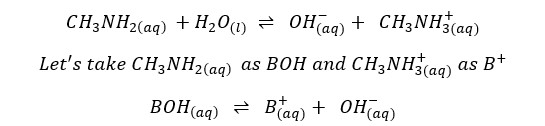
If you are given Ka instead of Kb for the dissociation of bases you can convert that into Kb using the below equation. This is necessary because you have to find the equilibrium constant of the forward reaction.
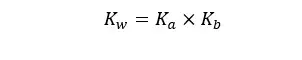
Back to the question:-
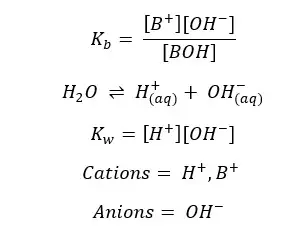
The charge should be balanced in the system
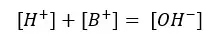
Let’s take [OH+] as x,
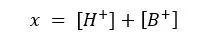
Because the initial concentration should be equal to the sum of products and reactants left,
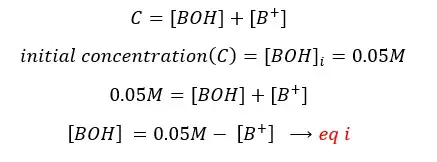
Assumption:
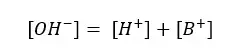
In the above situation, the solution gets H+ from the dissociation of water. But in the basic environment (extra OH- from the base) of the solution, that discourages the dissociation of water because according to the ‘le chatelier’s principle. (Because the solution has much greater [OH-] from the base. That will favor the backward reaction). So, when comparing [H+] with [B+], [H+] is a very small fraction.
So,
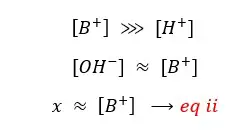
By substituting eq ii for [B+] in eq i,
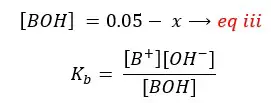
By substituting eq iii for [BOH], eq ii for [B+],

Concentration cannot be a negative value so,
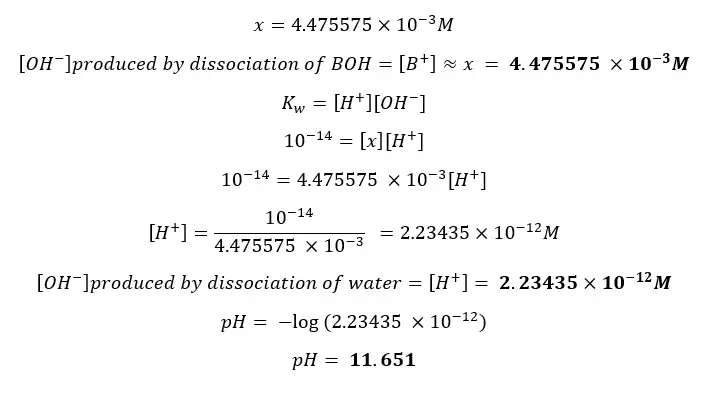

The cover image was created using an image by Gerd Altmann from Pixabay