Quantum Numbers - Principle, Azimuthal, Magnetic and Spin Quantum Numbers

Bhor's theory suggests that the electrons in an atom exist in the energy levels that have a unique energy. These energy levels are called principle energy levels or principle quantum numbers (n).

The frequency lines of the hydrogen spectrum consist of several thin lines. That means there are different frequency lines with slightly different frequencies present in a single frequency line. In 1916, a German theoretical physicist Arnold Sommerfield suggested that there are sub-energy levels that have slightly different energies in a principal energy level.

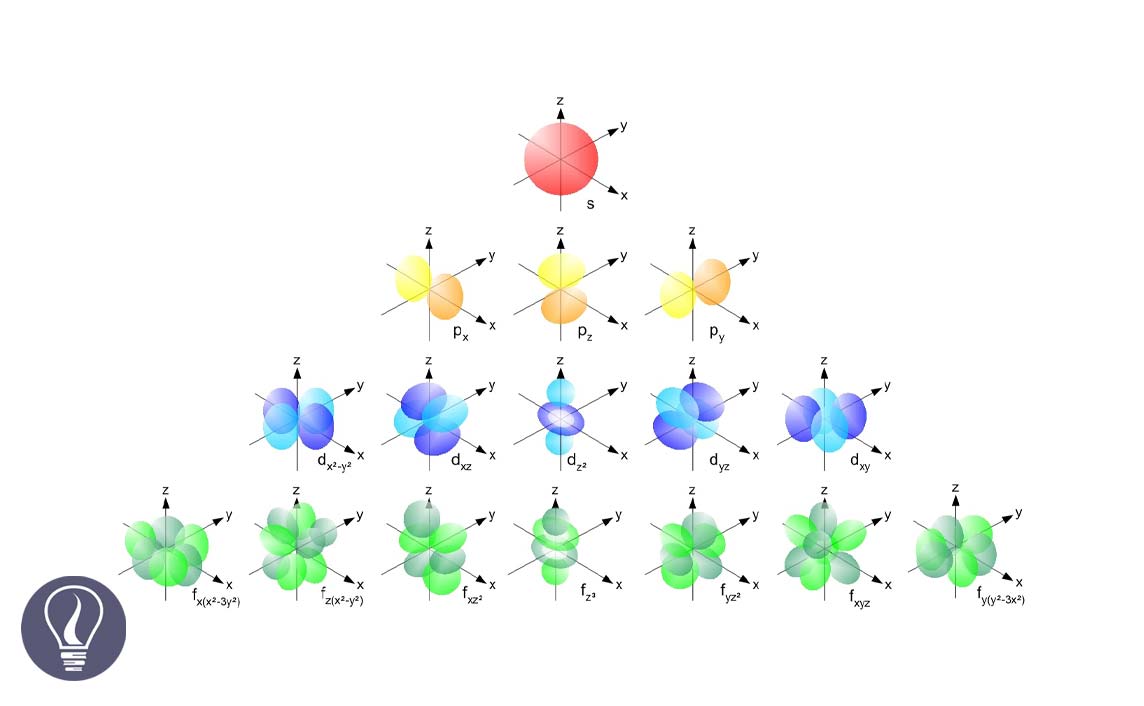
Subenergy levels are named s, p, d, f, g, …

A sub-energy level consists of atomic orbitals. Atomic orbital is where there is the highest probability that an electron can be found.

Four quantum numbers

According to the quantum theory that has been suggested by Austrian and naturalized Irish physicist Erwin Schrödinger, there are four quantum numbers that can describe the principle energy levels, sub-energy levels, and the atomic orbitals present in an atom.

1. Principle quantum number (n)
2. Azimuthal quantum number (l)
3. Magnetic quantum number (ml)
4. Spin quantum number (s / ms)

01. Principle quantum number (n)

The energy levels that exist around the nucleus of an atom are called the principal quantum number (n). The "n" can be 1, 2, 3, …. up to infinity.

That means there can be an infinite number of energy levels in an atom. The lowest energy level which is the nearest energy level to the nucleus, is n = 1.

02. Azimuthal quantum number (l)

Azimuthal quantum number (l) indicates the number of sub-energy levels present in a principal energy level. If the principal quantum number is n, the azimuthal quantum number is given by n - 1.

The number of sub-energy levels contained in a principle energy level is equal to the number of integers from 0 to n - 1.

Example:

• If an atom has 3 energy levels that means n = 3.
• n - 1 = 2
• So l would take all the integers within 0 to 2 including 0 and 2
• So l = 0, 1, 2
• This means this energy level contains 3 sub-energy levels

If n = 1,

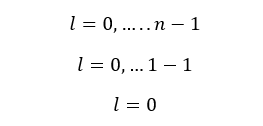
When n is 1,  l is equal to 0. That means there is only one value for l and that value is equal to 0. n = 1 is the first energy level (the innermost energy level - the energy level that is closest to the nucleus) of the atom.

This indicates that there is only one sub-energy level in the very first energy level of the atom. This sub-energy level is called the "s subshell".

When n is equal to 2,

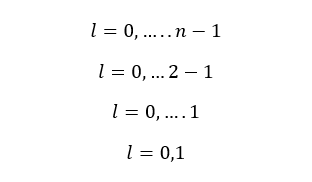
When n is equal to 2, there are two values for l. That means there are two subshells in the second principle energy level. Those subshells are s and p subshells.

When n is equal to 3,

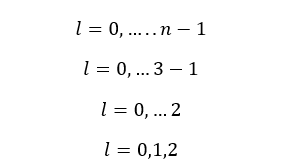
When n is equal to 3, there are three values for l. That means there are three subshells in the third principle energy level. Those subshells are s, p, and d subshells.

03. Magnetic quantum number (ml)

A subshell of an atom consists of atomic orbitals. The magnetic quantum number indicates the number of atomic orbitals present in a subshell. If a subshell is l, the magnetic quantum number is given by the number of integers from -l to +l.

If l is equal to 0,

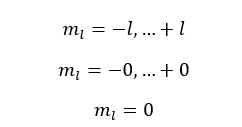
The l is equal to 0 means the s subshell. When l is 0,  only one value has been obtained for the magnetic quantum number. That means there is only one orbital in the 's subshell'.

If l is equal to 1,

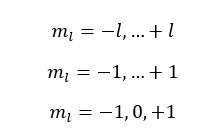
The l is equal to 1 means the p subshell. When l is 1, three values have been obtained for the magnetic quantum number. That means there are three atomic orbitals in the p subshell.

Those three orbitals are named px, py, and pz.

If l is equal to 2,

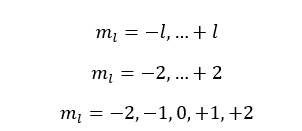
The l is equal to 2 means the d subshell. When l is 2, five values have been obtained for the magnetic quantum number. That means there are five atomic orbitals in the 'd subshell'.

Those five orbitals are named as dxy, dyz, dxz, dx^2-y², dy².

04. Spin quantum number (s / ms)

The spin quantum number indicates the number of electrons that exist in an orbital. For each magnetic quantum number, there are only two values are obtained from the spin quantum number.

Those obtained values are +1/2 and -1/2. That means the number of electrons present in an atomic orbital is two.

Quantum number set of an electron in an atom

An electron in an atom has a unique quantum number set. Using the four quantum numbers, the principal energy level, the subshell, and the orbital where the electron exists can be represented.

As an example, the quantum number set for the electron that is present in a Hydrogen atom at the ground state can be represented as follows.

• The electron in a hydrogen atom at the ground state exists in 1s orbital. Therefore, the principal quantum number (n) is 1.
• That means the first energy level. In the first energy level, there is only one subshell which is s subshell.
• Therefore, the azimuthal quantum number (l) is equal to 0.
• There is only one atomic orbital in the 's' subshell. Therefore, the magnetic quantum number (ms) is also 0.
• The quantum number set for the electron that is present in a Hydrogen atom: (1, 0, 0, +1/2 or -1/2)