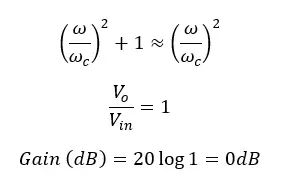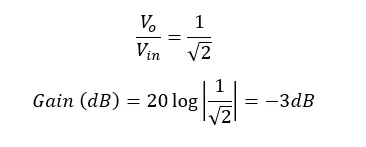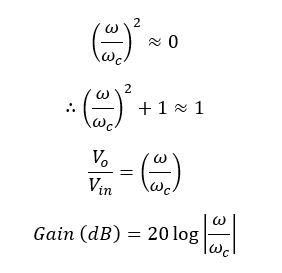High-Pass Filters (HPF) - Active High Pass Filter and Passive High Pass Filter

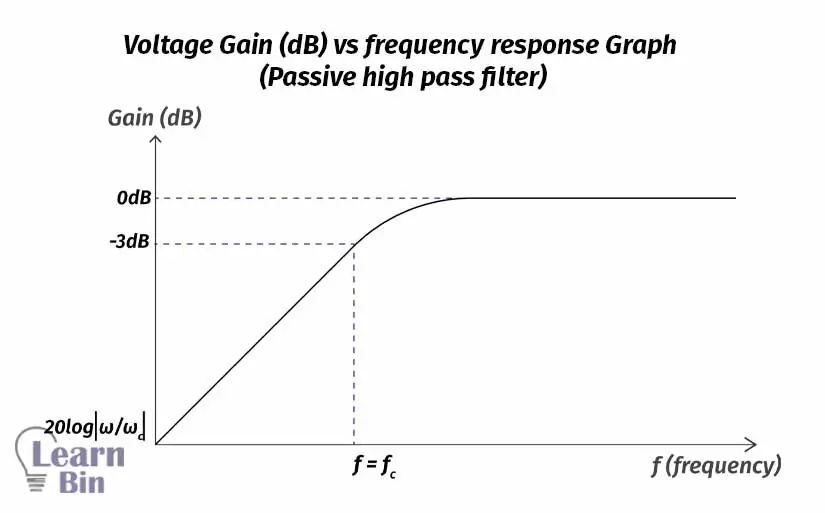
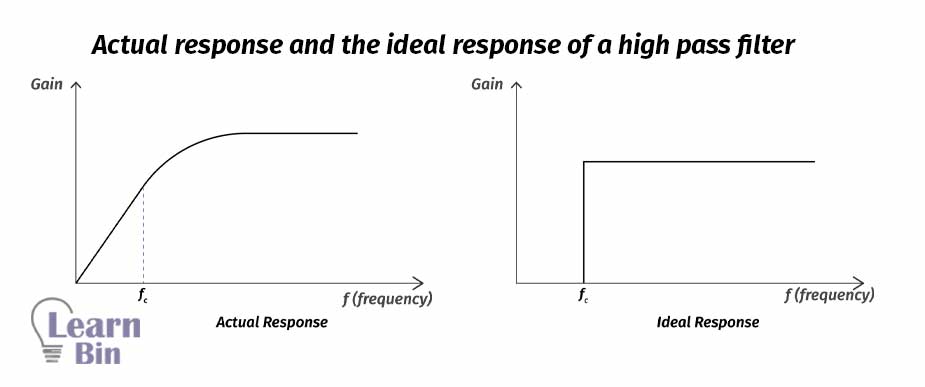
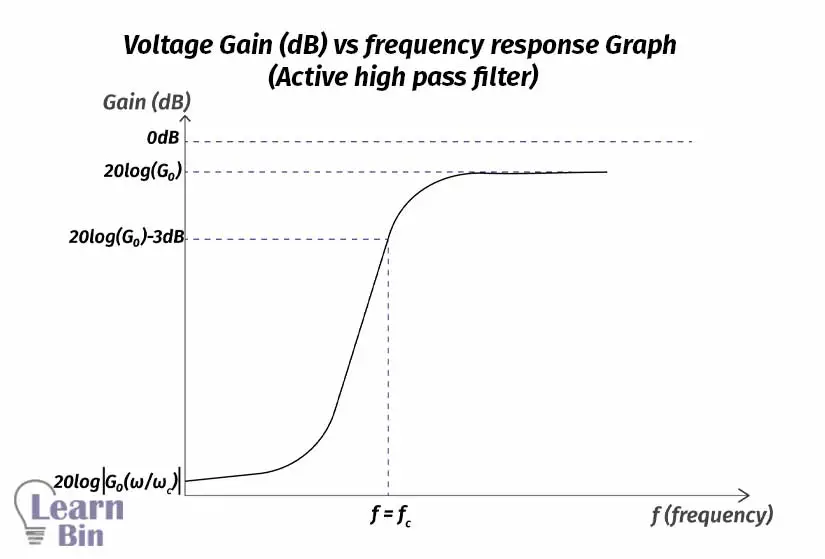
A high-pass filter is a filter that significantly attenuates or rejects all frequencies below f_c (critical frequency) and passes all frequencies above f_c. The pass band of a high-pass filter is all frequencies above the critical frequency.

Active high pass filters

Calculation of transfer function of an active high-pass filter

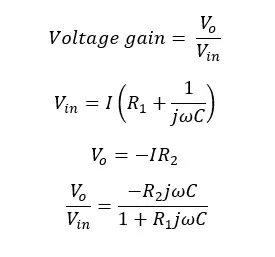
Let’s take,

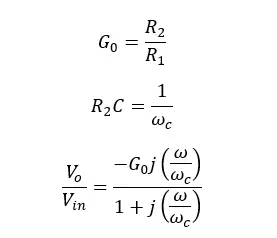
To remove complex numbers in the equation, the 4^th power of the complex part is taken and takes the 4^th root. This mathematical operation can be done separately for two complex parts.

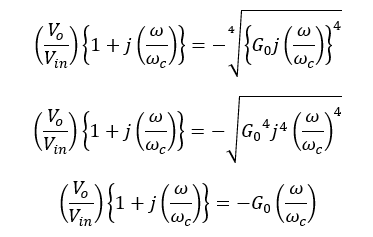
To remove the other complex part in the equation, the same operation can be done.

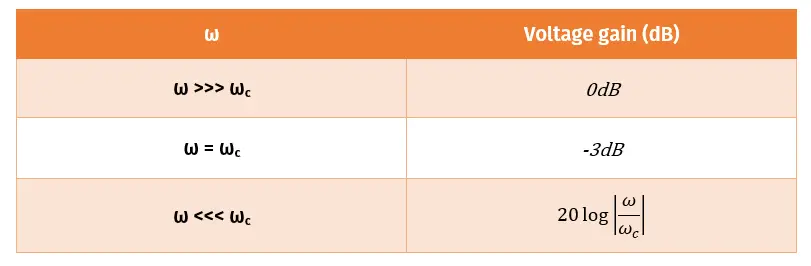
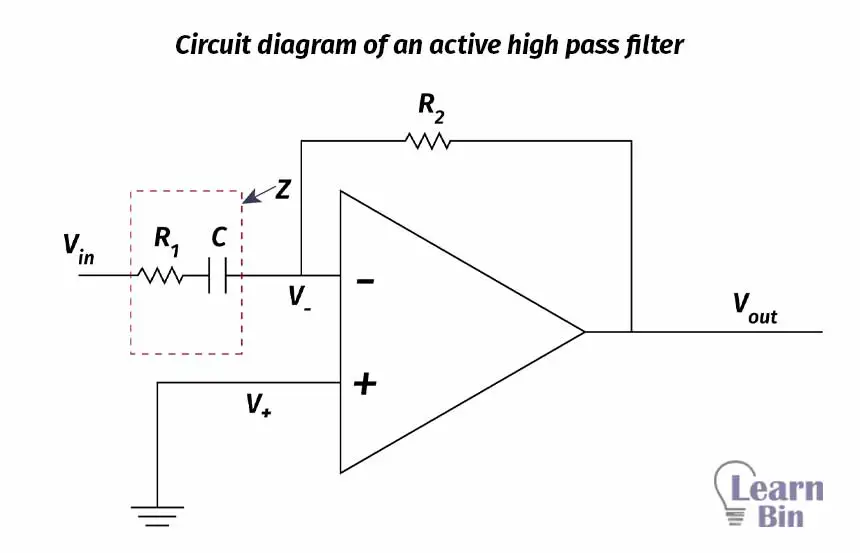
Therefore, the voltage gain of an active high pass filter can be written in,

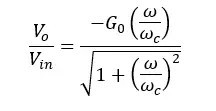
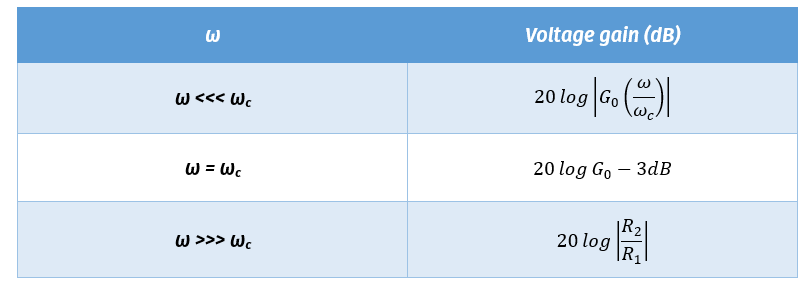
The above equation gives the transfer function of an active high-pass filter. The voltage gain at each ω (Angular frequency of the signal) value can be calculated using the above equation.

Calculation of voltage gain at different ω (frequency) values using the transfer function of an active high-pass filter

• When ω <<< ω_c

• When ω = ω_c

• When ω >>> ω_c

Passive high pass filters

Calculation of transfer function of a passive high-pass filter

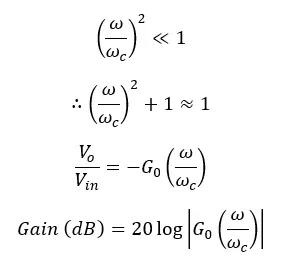
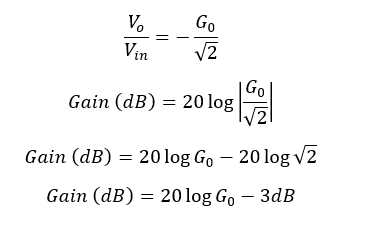
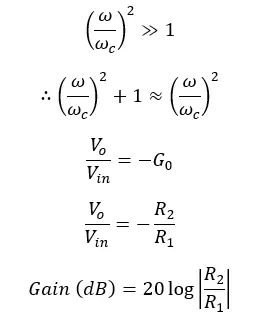
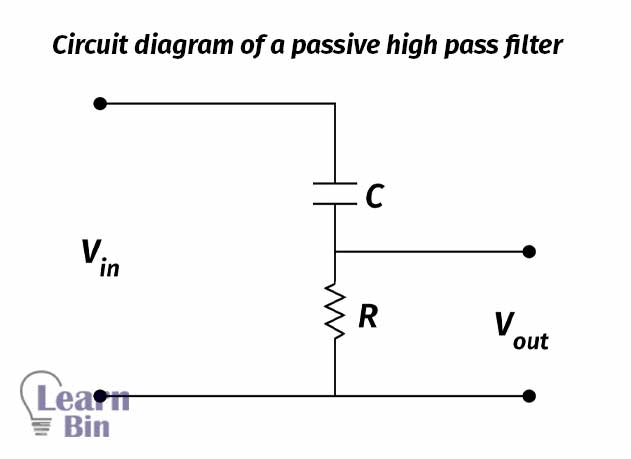
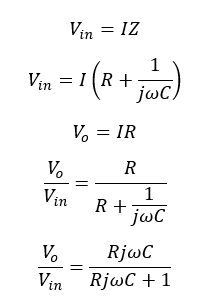
Take

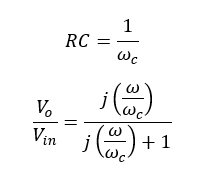
To remove the complex part in the equation, the same operation that was done on the transfer function in the active filter can be used here.

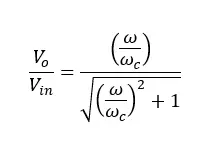
The above equation gives the transfer function of a passive high-pass filter. The voltage gain at each ω (Angular frequency of the signal) value of a passive high-pass filter can be calculated using the above equation.

Calculation of voltage gain at different ω (frequency) values using the transfer function of a passive high-pass filter

• When ω >>> ω_c

• When ω = ω_c

• When ω <<< ω_c