More results...


Motion is a change of position of an object. A motion can be an absolute motion or a relative motion. Absolute motion is just a change of position of an object.
When a motion is observed, the observer's frame is known as the reference frame. Motion that happens relative to the observer (Reference frame) can be defined as relative motion.
We should measure the physical quantities of the object with respect to the reference frame.
E.g.,
When measuring relative physical quantities of motion, it is simply the difference between the physical quantity of the object and the reference frame.
Let's assume that there are two objects A and B. The velocities of A and B are VA and VB respectively. So, we can write the relative velocity of B with respect to A as follows.
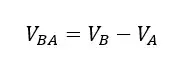
Where,
Here, VA and VB are measured relative to the earth. We assume that the earth is a stationary frame. In the same way, we can write an equation for relative acceleration for two accelerating objects as follows.
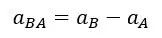
Where,
Let's imagine that two cars of A and B start to move on a straight road at the same initial position. Velocities of A and B are 40 ms-1 and 50 ms-1 respectively. Both cars are moving in the same direction.
We can find the relative velocities of each car as follows.
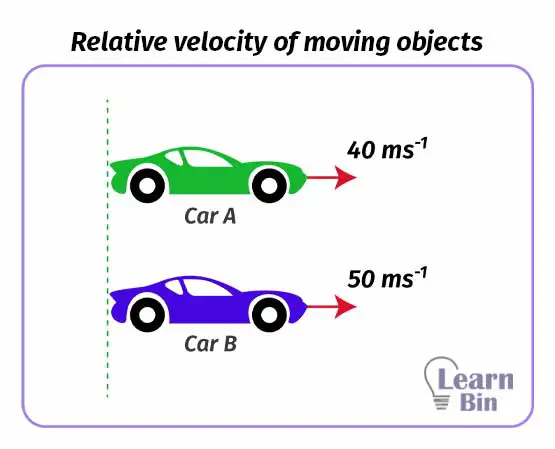
First, we take a situation where a person in car A, is observing car B. Here, the reference frame is car A.
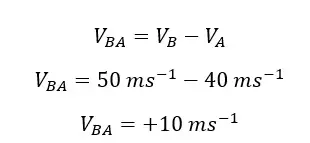
The relative velocity of B, with respect to A, is +10 ms-1. This means that when we observe car B from car A, we can observe that car B is moving 10 ms-1 faster than car A (reference frame).
Now let's find the velocity of A with respect to B.
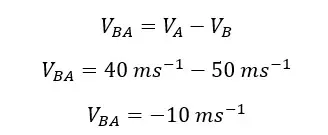
In this situation, the reference frame is car B. (We are observing car A from car B). The relative velocity of A, with respect to B, is -10 ms-1. This means that when we observe car A from car B, we can observe that car A is moving 10 ms-1 slower than car B.
But if we observe both cars from the ground (earth) we can see car A is moving at 40 ms-1 and car B is moving at 50 ms-1. This is because we are observing from the earth and we take the earth as a stationary frame.
Now, let's imagine a situation above where two cars of A and B are moving towards each other at velocities of 40 ms-1 and 50 ms-1 respectively. Since the velocity is a vector, we should consider the direction of the motion also.
If we assume that car A is moving in the positive direction, car B is moving in the negative direction. So, the velocities of car A and car B are 40 ms-1 and -50 ms-1 respectively.
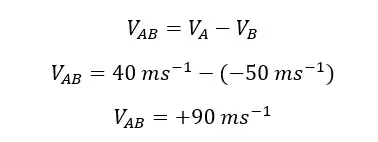
This indicates that the velocity of car A when observed from car B is +90 ms-1. That means if we assume that car B is stationary, we can observe that car A is moving at 90 ms-1 velocity towards car B. Positive sign indicates that car A is moving in a positive direction. The distance between two cars decreases by 90 m for every second.
We can calculate the velocity of B with respect to A as follows,
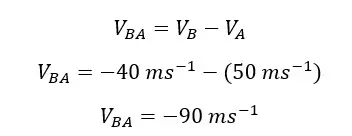
This indicates that the velocity of car B when observing from car A is -90 ms-1. That means if we assume that car A is stationary, we can observe that car B is moving at 90 ms-1 velocity towards car B. Negative sign indicates that car B is moving in the negative direction.
Now let's imagine two cars of A and B are moving towards each other at velocities of 40 ms-1 and 50 ms-1 respectively. A person in car A is throwing a ball (object C) at 10 ms-1 velocity in the positive direction (towards car B). The velocity of the ball C is measured with respect to the car A.
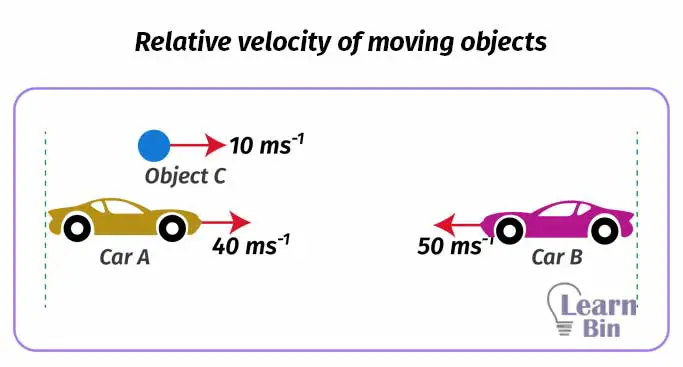
Let's find the velocity of the ball C with respect to the car B. The velocity of ball C is given with respect to car A. So, first, we should find the velocity of ball C with respect to the earth.
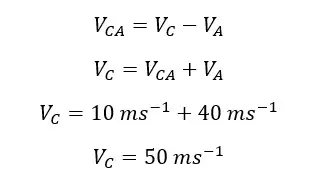
The velocity of the ball C with respect to the earth is 50 ms-1. It is given by the total of the velocity of car A and the ball C.
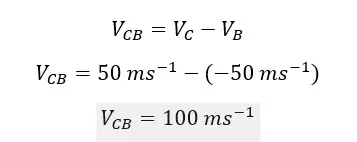
This means when we observe from car B, and if we assume that car B is stationary, the velocity of the ball is 100 ms-1.
