More results...


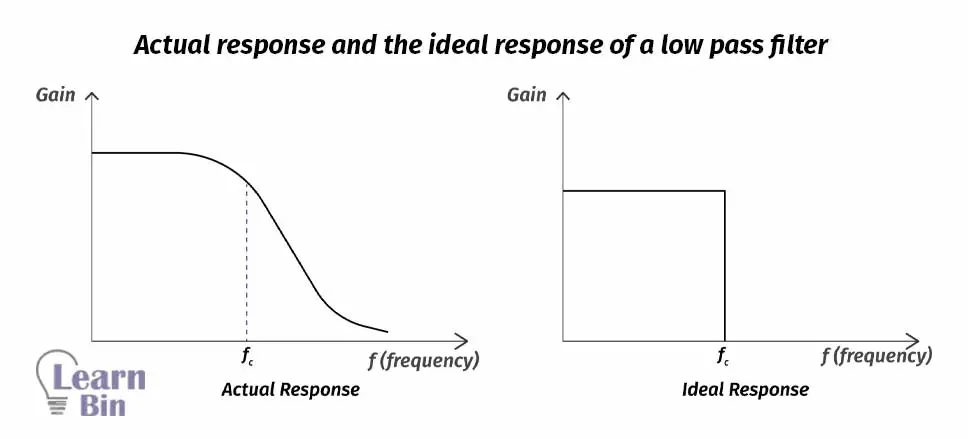
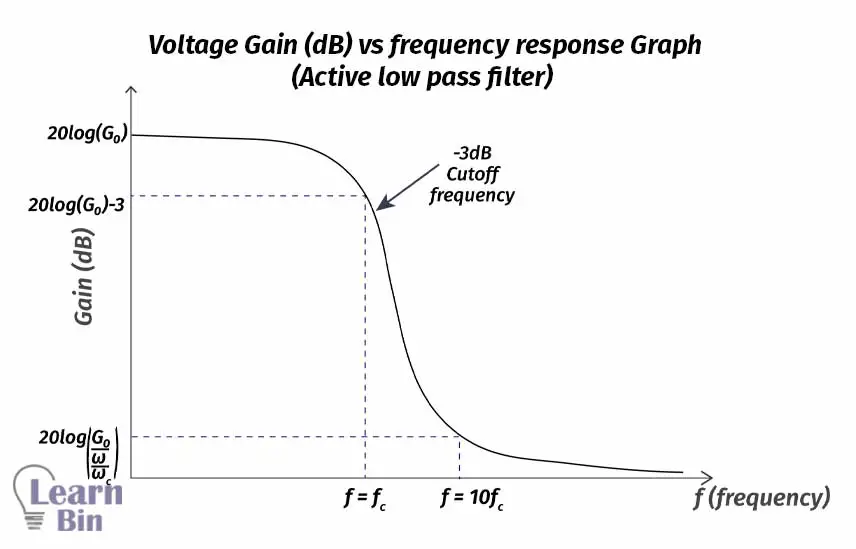
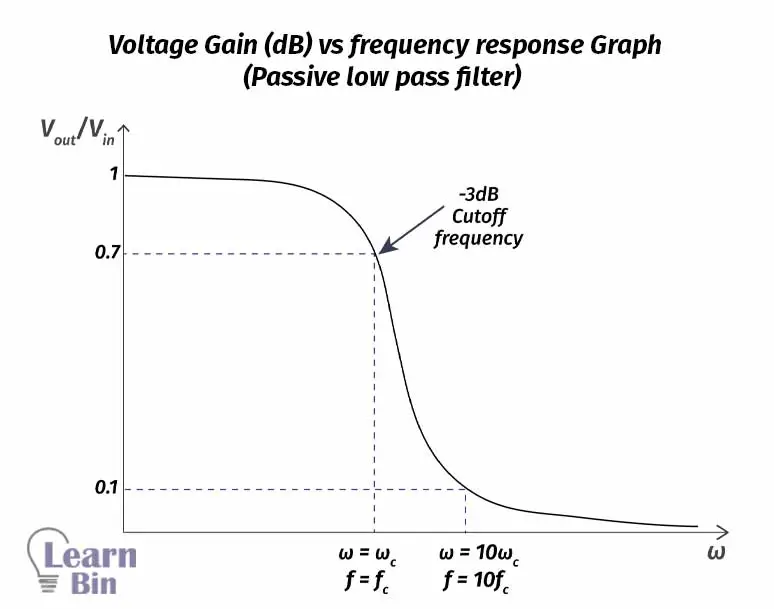
A low pass filter is a filter that passes frequencies from 0Hz to critical frequency, fc, and significantly attenuates all other frequencies.
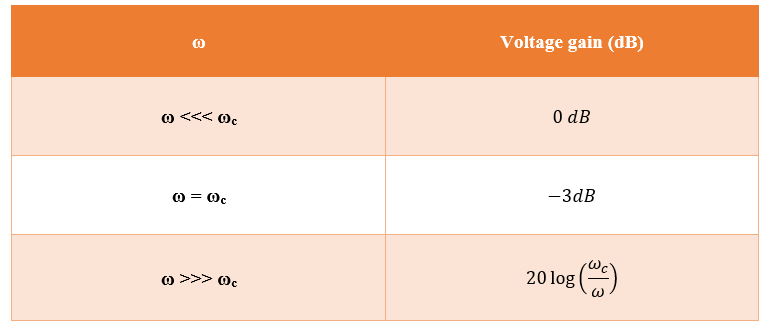
At low frequencies, XC (Impedance given by the capacitor) is very high, and the capacitor circuit can be considered an open circuit. So under this condition, Vout= Vin or Gain = 1.
At very high frequencies, XC is very low, and the Vout is small as compared with Vin. Hence the gain falls and drops off gradually as the frequency is increased.

The voltage gain of an active low pass filter can be calculated as follows,
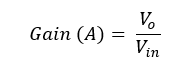
To construct this filter, we are using 741 op-amp. Here, noninverting input (V+) input has been grounded. Therefore, the voltage at V+ is zero. There is no voltage difference between the noninverting input (V+) and the inverting input (V-). So, the voltage at inverting input V- is also zero. According to Ohm’s low, Vin can be given by,
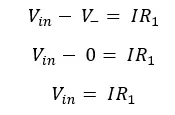
To calculate Vo, the total impedance (Z) given by resistor (R2)and capacitor (C) should be calculated.
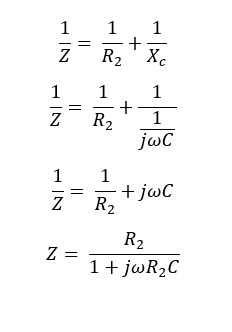
Where,
According to Ohm’s law, Vo is given by,
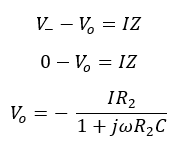
Let’s take
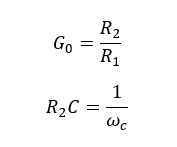
Where,
So, the voltage gain is given by,
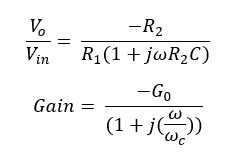
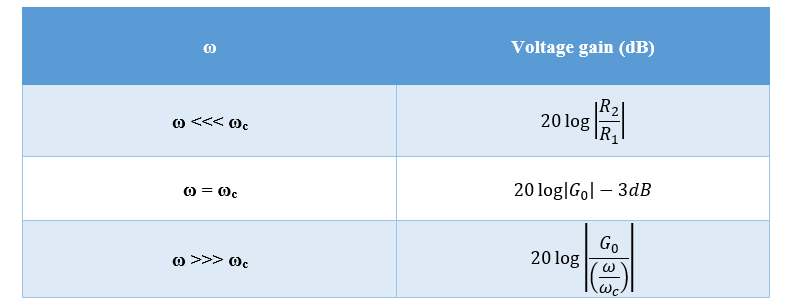
The above equation is the transfer function of an active low-pass filter. Using this equation, the voltage gain at each ω (Angular frequency of the signal) value can be calculated.
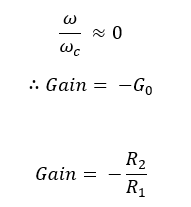
The voltage gain is expressed in decibels (dB).
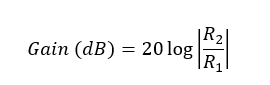
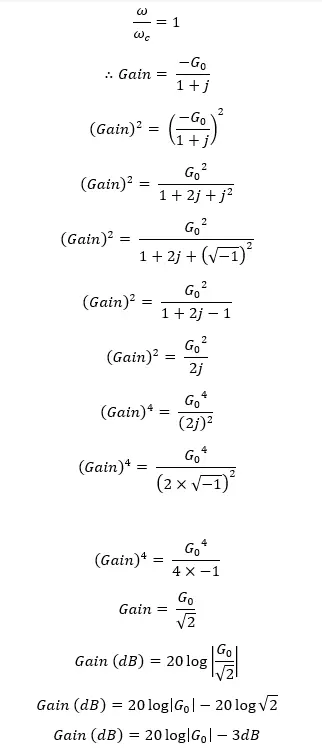
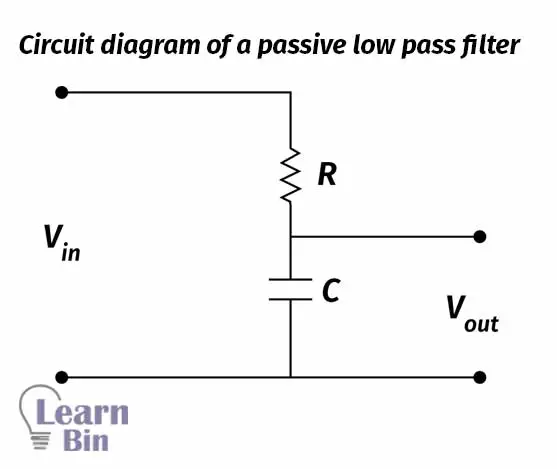
The voltage gain of a passive low pass filter can be calculated as follows,
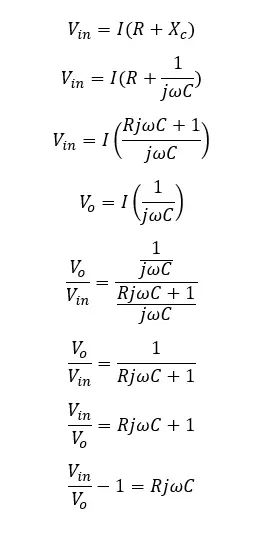
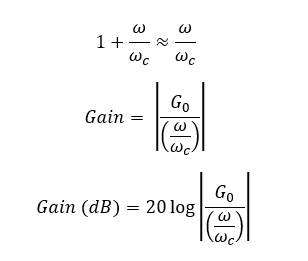
Let’s take
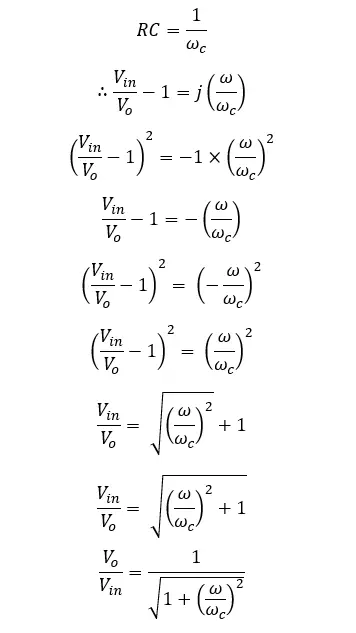
The above equation is the transfer function of a passive low-pass filter. Using this equation, the voltage gain at each ω (Angular frequency of the signal) value can be calculated.
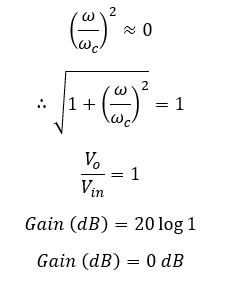
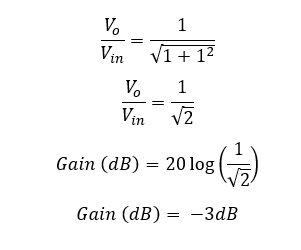
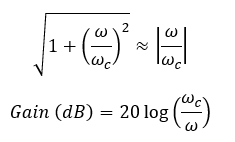

The cover image was created using an image by Marijn Hubert from Pixabay