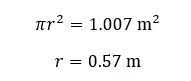More results...


In a previous article, in there we discussed the thermal expansion of solids and the linear expansion of solids. In this article, we will discuss the superficial expansion of solids.
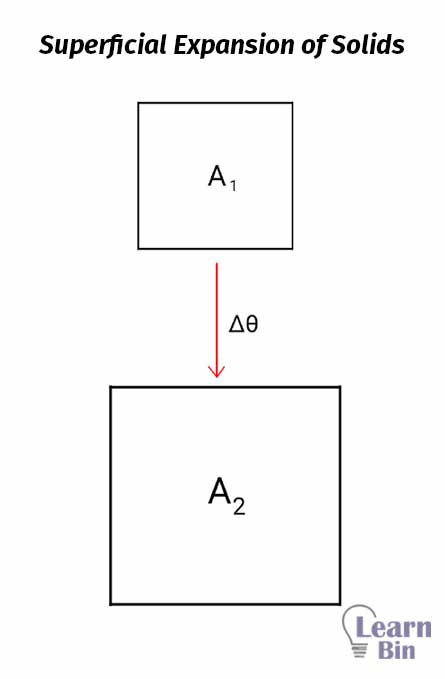
A sheet-like object (consider a sheet of metal) is heated, and it will show an increase in surface area. This is known as the superficial expansion of solids.
Mathematically, if a sheet-like object with a surface area of A1 takes the area of A2 when the temperature is increased from θ1 to θ2, the increase in area is proportional to the initial area and the temperature difference.

Where,
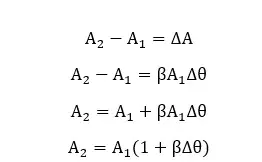
The coefficient of superficial expansion is a proportional coefficient. It is known as the rational increase in area when the temperature is increased by 1° of Celsius or Kelvin.
The coefficient of superficial expansion is a constant for a particular material. If the material is isotropic, the coefficient of superficial expansion can be expressed in terms of linear expansion coefficient.
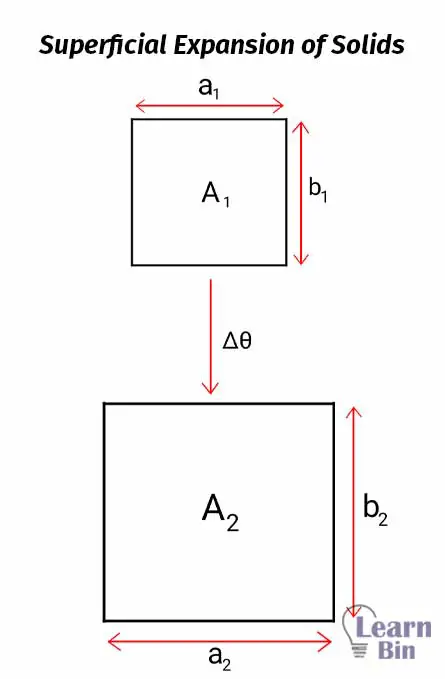
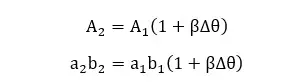
According to the linear expansion of matter,
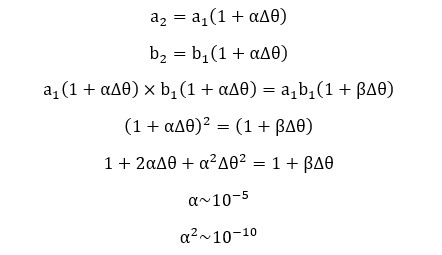
When compared to α, α2 too small, therefore α2Δθ2 is negligible. The equation can be written as follows.
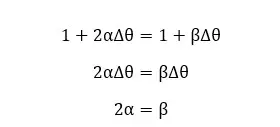
According to the above equation, the coefficient of superficial expansion is twice the linear expansion coefficient if the material is isotropic. That means all the properties of the material are the same in every direction.
Question 01
A square-shaped thin aluminum sheet with a side length of 4 m is heated at 300°C. There is a circular hole in the aluminum sheet with an area of 1 m2. Find the aluminum sheet's new surface area and the hole's new radius. (coefficient of superficial expansion of aluminum is 2.3 ×10-5 °C)
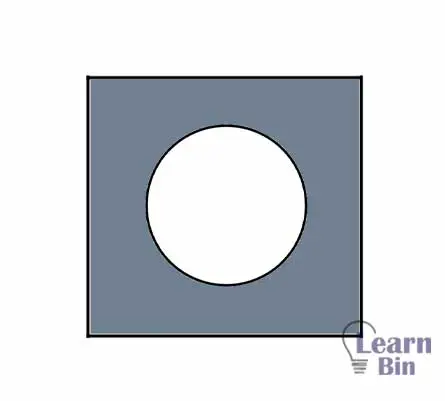
Solution
When heating, the hole is also expanded as the way a sheet with the same area expands. Therefore, the radius of the hole is increased. The final area of the aluminum sheet would be the difference between the expanded square sheet and the area of the expanded hole. Area of the expanded aluminum sheet,
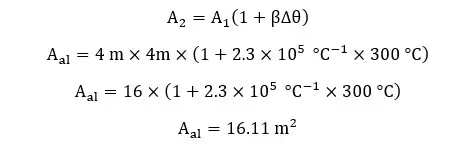
Area of the hole
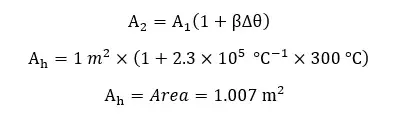
The new area of the aluminum sheet

New radius of the hole