Upthrust, Buoyancy, and Buoyant Force

Upthrust

When an object is completely or partially submerged in a fluid, the upward force exerted by the fluid on the object is called Upthrust. Upthrust is also called the Buoyant force.

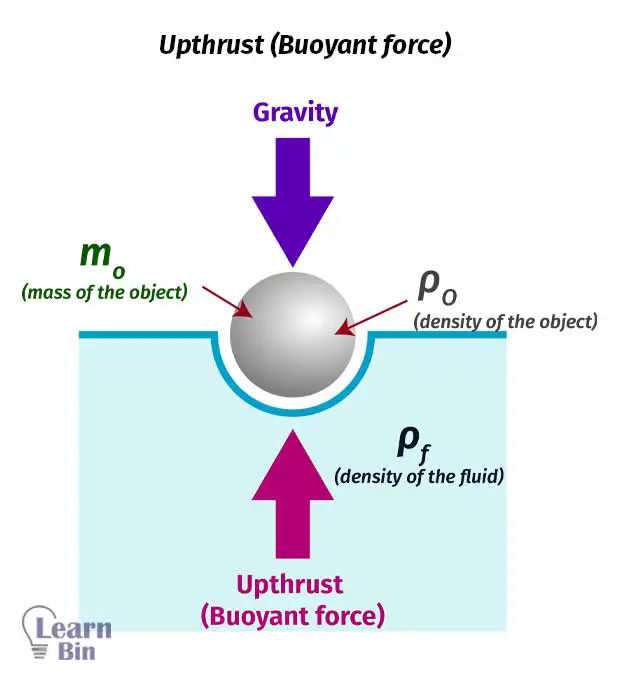
Upthrust is the resultant force of the forces due to the fluid pressure on each point of the object. If we consider a cubic object, the forces due to the fluid pressure on side surfaces are the same and opposite in direction.

Therefore, the forces on the side surfaces will be canceled out. The force on the lower surface is higher than the force on the upper surface. Therefore, there is an upward resultant force. This force is the upthrust.

Buoyancy

Buoyancy is the tendency of an object to float in a fluid (liquid or gas). As described in the above section, there are forces that act on an object that is immersed in a fluid. Buoyancy occurs because of the effect of these forces. The buoyancy of an object depends on factors such as,

• Weight of the object
• Density of the fluid
• Size of the object
• Shape of the object
• Density of the object

When the density of a fluid is increased, that will increase the buoyancy effect of the fluid.

Center of buoyancy

The center of buoyance is the point at which the upthrust force acts. The center of buoyancy is located at the center of gravity, of the volume displaced by the object.

Archimedes principle

When an object is completely or partially submerged in a still, incompressible fluid, the upthrust act on the object is equal to the weight of the volume of fluid that is displaced by the object.

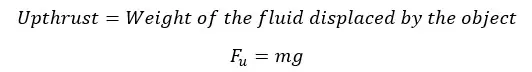
Where,

• F_u = upthrust
• m = mass of the object
• g = gravitational acceleration

Proving the Archimedes principle

Consider a situation where an object is completely immersed in a fluid and remains at rest. The object remaining at rest means that the forces acting on the object are balanced. Therefore,

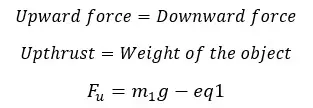
Where

• m₁ - the mass of the object.

Before the object is submerged in the fluid, there is a fluid volume that has the exact shape of the object. The upthrust also acts on this fluid volume. If the mass of the fluid volume is m₂, we can write the expression for upthrust as follows,

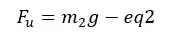
From equation 1 and 2,

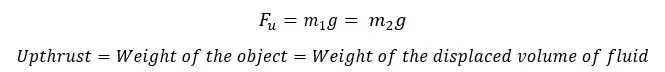
If the displaced volume of the fluid is V, and the density of the fluid is ρ, we can write this expression in terms of density.

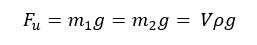
Where,

• F_u = Upthrust
• m₁ = Mass of the object
• m₂ = Mass of the displaced volume of the fluid
• V = Displaced volume of the fluid
• ρ = Density of the fluid
• g = Gravitational acceleration

Examples of upthrust test questions

Examples of upthrust test questions - Question 01

A thick wooden block is floating on water. If 1/3 of the wooden block is submerged in water and remains at rest, find the relative density of the wooden block.

• Solution

Let's take the densities of the wooden block and water are d₁ and d₂ respectively. The volume of the wooden block is V. If 1/3 of the volume is submerged in water, the displaced volume is 1/3 V.

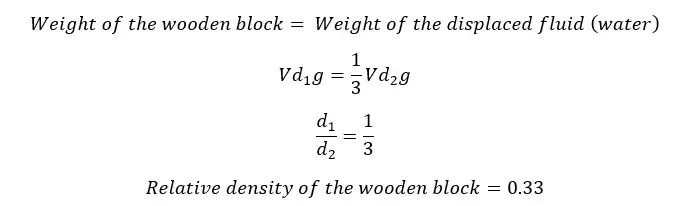
Examples of upthrust test questions - Question 02

When a wooden block is submerged in water, 2/3 of its volume is submerged. When the same wooden block is submerged in an unknown liquid 3/5 of its volume is submerged. Find the relative density of the unknown liquid.

• Solution

Let's take the upthrust forces given by water and the unknown fluid are F₁ and F₂ respectively. If the mass of the wooden block is m, the upthrust forces in water and the unknown liquid can be written as follows.

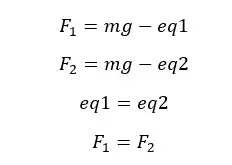
If the volume of the wooden block is V the densities of water and the unknown liquid are d₁ and d₂, we can write an expression for upthrust in terms of density.

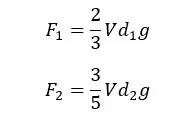
Since the upthrust forces are equal in both situations,

Hydrometer

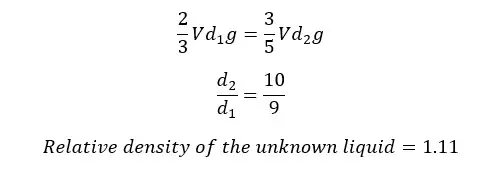
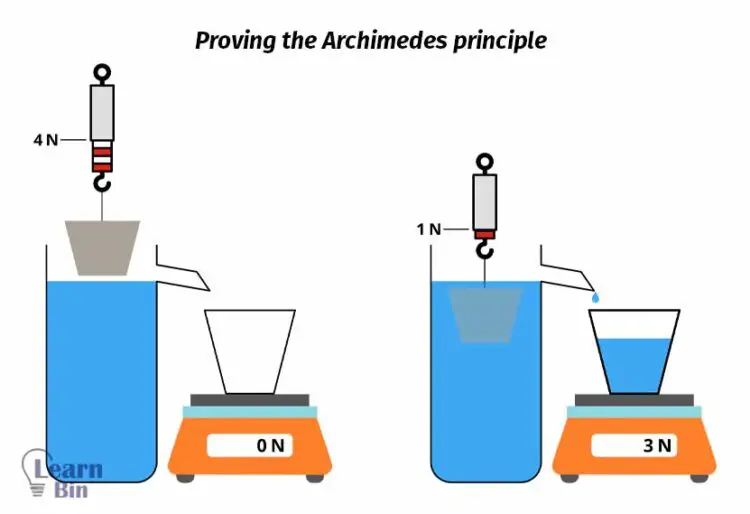
A hydrometer is used to find the density or the relative density of a liquid. A hydrometer works on the principle of buoyancy. A mass is attached to the bottom of the hydrometer. Due to this mass, the center of gravity will be lower than the center of buoyancy.

Therefore, the hydrometer stays vertical. The bottom of the hydrometer is shaped like a bulb. As a result, a larger volume of fluid is displaced from a smaller height. Due to this, the height of the immersion of the hydrometer is reduced.

According to the Archimedes principle,

Where,

• M = Mass of the hydrometer
• ρ = Density of the liquid
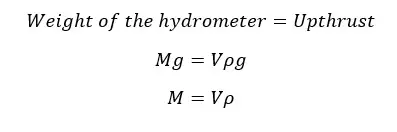
• V = Submerged volume

In the above equation, the mass of the hydrometer is constant. Therefore,

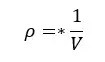
When the density of the fluid is high, the liquid volume displaced by the hydrometer is low. Therefore, the readings of the hydrometer are numbered from top to bottom.