More results...


Material balance calculation is a necessary thing in chemical engineering. Material balance or mass balance is the calculation of the amount of each component at the inputs and outputs in every process step.
Before material balance calculation, we should have a proper idea about a system, system boundary, and surrounding. A system is a region or a quantity of matter that we have chosen to study. Anything outside of the system is surrounding. The real or imaginary surface that separates the system from its surroundings is the boundary.
In an industrial process, we insert materials into a system and products are taken out of the system. In material balance calculation, we calculate the percentages or masses of what we input and what we get from the output.
Calculation of material balance for an entire process is a complex task. Therefore, we calculate the material balance for every single process step. The general material balance equation is as follows.
Material in + Generation = Material out + Consumption + Acuumulation

Material balance can be applied to the total mass or total moles of the stream, the mass of a single compound, the mass of an atomic species, the moles of a compound, the moles of an atomic species, etc.
There are processes with or without a chemical reaction and steady and unsteady processes. According to the type of the process, the above equation is changed.
Material in + Generation = Material out + Consumption + Accumulation
Material in + Generation = Material out + Consumption
Material in =Material out + Accumulation
Material in =Material out
Let’s consider a recovery process of ethanol from a gas mixture that contains air, water vapor, and ethanol vapor. We are going to separate ethanol from gas. Before calculating the material balance, the first step that should be done is to prepare a flow diagram for the process. The simple flow diagram for the above process is as follows.
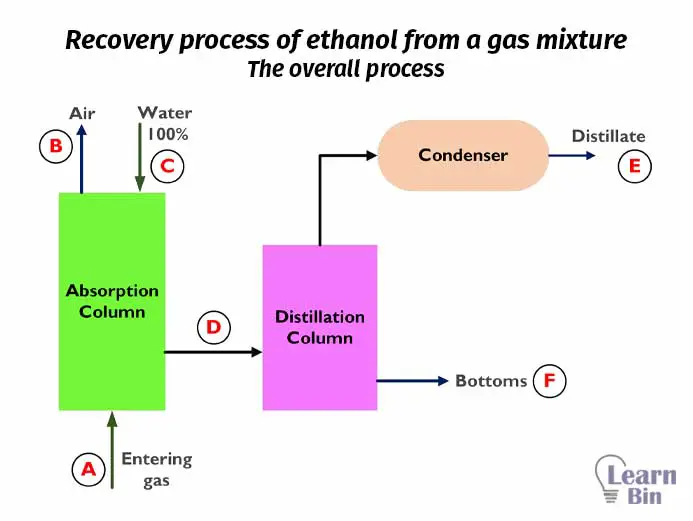
In the above process, there are no chemical reactions. Both absorption and distillation are physical separation methods. Therefore, in this process, there is no material generation or consumption. If we consider this process operates at a steady state, there is no material accumulation. For ease of calculation, the overall process can be divided into two systems.
The first system is the absorption column. For the absorption column, there are two inputs and two outputs. The mass percentages of each input and output of the absorption column are as follows.
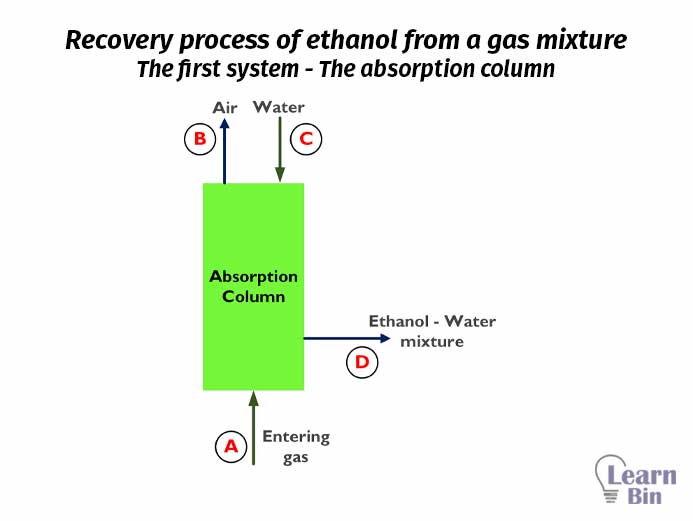
| Stream | Water | Air | Ethanol |
| Stream – A Input gas | 2% | 95% | 3% |
| Stream – B Output gas | 0.5% | 99.5% | 0% |
| Stream – C Input water | 100% | 0% | 0% |
| Stream – D Output water | 81% | 0% | 19% |
If the input gas flow rate is 1000 Kg/hr, we can calculate the masses of each component of each stream using material balance. Each component of the system (water, air, ethanol) is applied to the mass balance separately.
A, B, C, and D are the flow rates of each stream. Since this process is not include a chemical reaction and operates at a steady state, the material balance equation would be,
Material in = Material out
A + C = B + D
Air
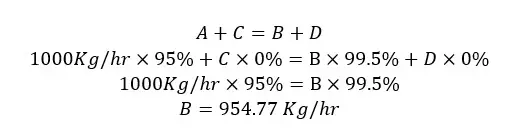
Ethanol
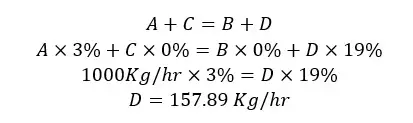
Water
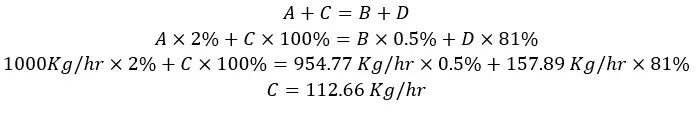
For the above system input and output flow rates can be summarized as follows.
| Stream | Flow rate (Kg/hr) |
| Stream – A Input gas | 1000 |
| Stream – B Output gas | 954.77 |
| Stream – C Input water | 112.66 |
| Stream – D Output water | 157.89 |
We take both the distillation column and condenser as the second system. For this system, there are one input and two outputs. The mass percentages of each input and output of this system are,
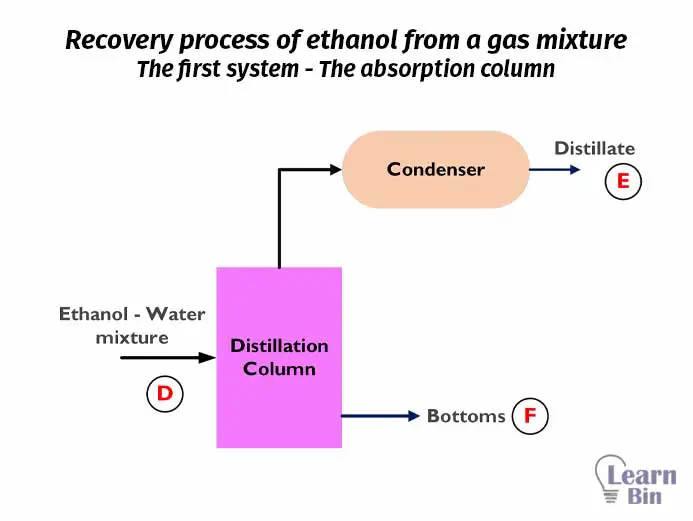
| Stream | Water | Ethanol |
| Stream – D Input ethanol-water mixture | 81% | 19% |
| Stream – E Output distillate | 1% | 99% |
| Stream – F Output bottoms | 96% | 4% |
Material in = Material out
D = E + F
Ethanol
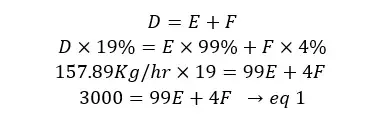
Water
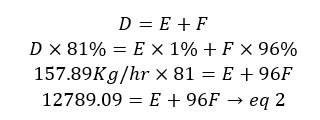
By solving the above two simultaneous equations (eq1 and eq2) we can calculate the flow rates of E and F.

By substitution of the above value to equation 2, we can calculate the value of F.

For system 2, input and output flow rates can be summarized as follows.
| Stream | Flow rate (Kg/hr) |
| Stream – D Input ethanol-water mixture | 157.89 |
| Stream – E Output distillate | 24.93 |
| Stream – F Output bottoms | 132.96 |
In processes where a chemical reaction is included, new materials are generated, and some materials are consumed in the system. Therefore, output materials are not similar to input materials. So, input masses are not equal to the output masses of materials. In this situation, it is easy to use the mole balance of components.
Let’s consider the H2SO4 manufacturing process. The overall process can be simplified as follows. This process includes chemical reactions.
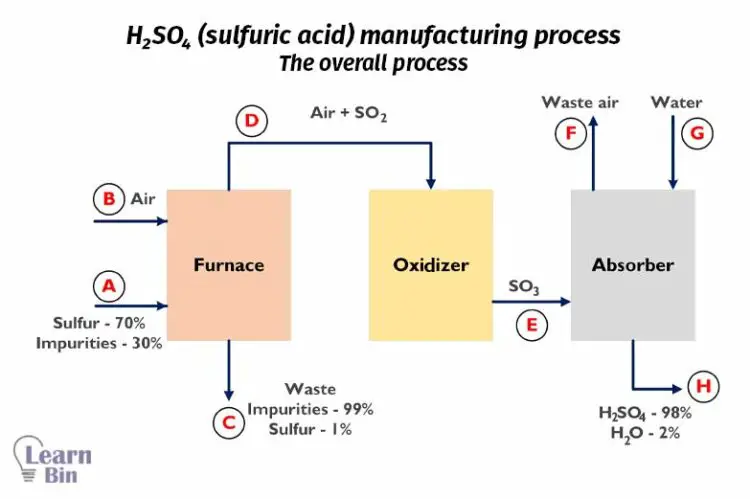
First sulfur is burned in a furnace and results in SO3. Input sulfur has 70% purity with 30% of inert impurities. The flow rate of input sulfur is 2000 Kg/hr.
In the furnace, 99% of sulfur is converted to SO2, and the SO2 + air mixture is passed to the oxidizer. At the oxidizer, SO2 is converted into SO3 gas.
At the absorber, SO3 gas is absorbed by water resulting in 98% of H2SO4. The chemical reactions at each step are given below.
At furnace
S + O2 → SO2
At oxidizer
2SO2 + O2 → 2SO3
At absorber
SO3 + H2O → H2SO4
By finding the moles of one component, we can find the moles and the masses needed for all the components. We are dividing the overall process into sub-systems for ease of calculation. All the calculations are done for a one-hour process window.
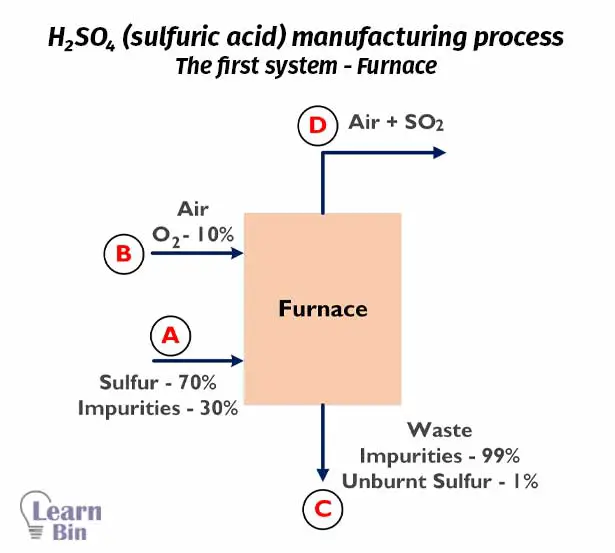
The furnace has two inputs and two outputs.

Total from the total mols of sulfur, 99% is converted into SO2. Only 1% is removed with impurities.
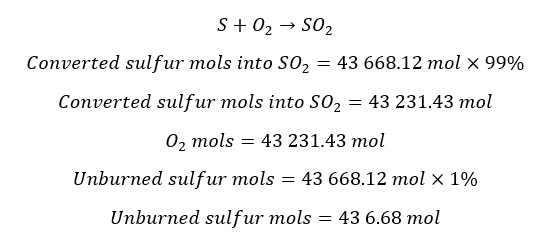
43 231.43 mols of SO2 gas was inserted into the Oxidizer. If we consider the oxidizer is 100% efficient, the total SO2 will be converted to SO3.
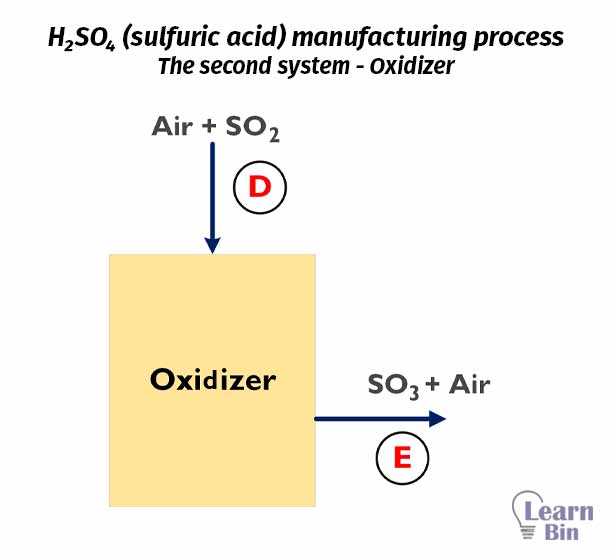
2SO2 + O2 → 2SO3
According to the stoichiometry, generated SO3 mols are equal to SO2 mols.
SO3 mols = 43 231.43 mol
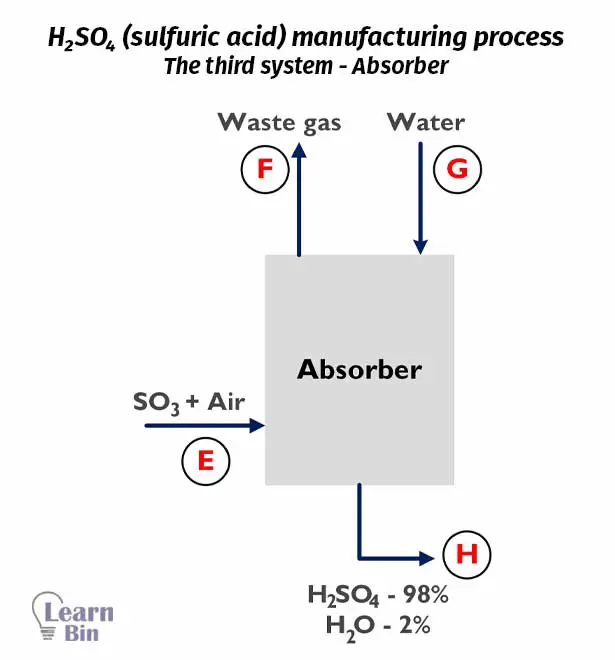
Water and output air (SO3 + Air) from the oxidizer was inserted into the Absorbe. At the absorber, SO3 gas is absorbed by H2O resulting in 98% of H2SO4.
The amount of entering SO3 mols into the absorber is 43 231.43 mol.
SO3 + H2O → H2SO4
According to the stoichiometry, mols of SO3 are equal to the mols of H2SO4 mols produced. Therefore,
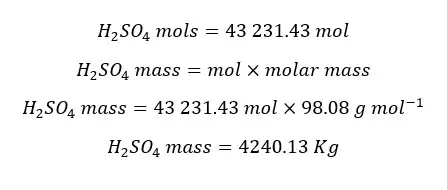
In the output stream of H, there is only 98% of H2SO4. The total mass of the output stream of H per hour is as follows.

In the absorption column, there is no generation of H2O. Therefore, it would be zero. Consumed mols of water are equal to the consumed mols of SO3.
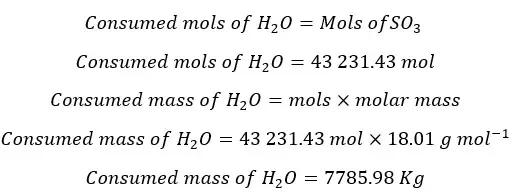
Mass balance for H2O


The cover image was designed using an image by Mediamodifier from Pixabay
Why it is so tough for me 😥?
I am a first year chemical Engineering student.
Thank you. You explained it very nicely.
The mass balance was well presented and clarified a lot of questions