More results...


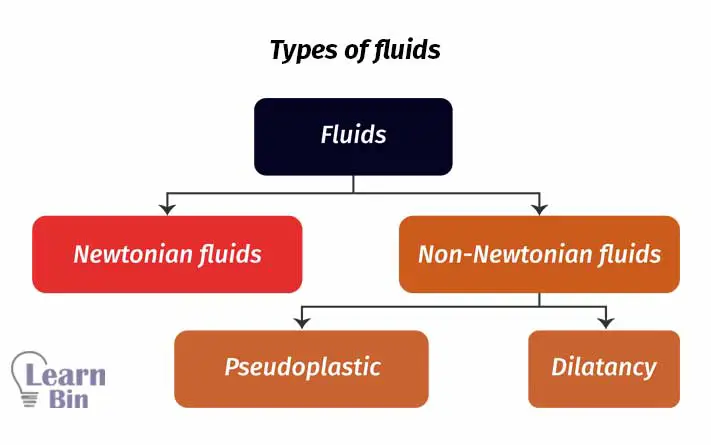
Fluids can be divided into two categories based on the change in their viscosity when shear is applied.
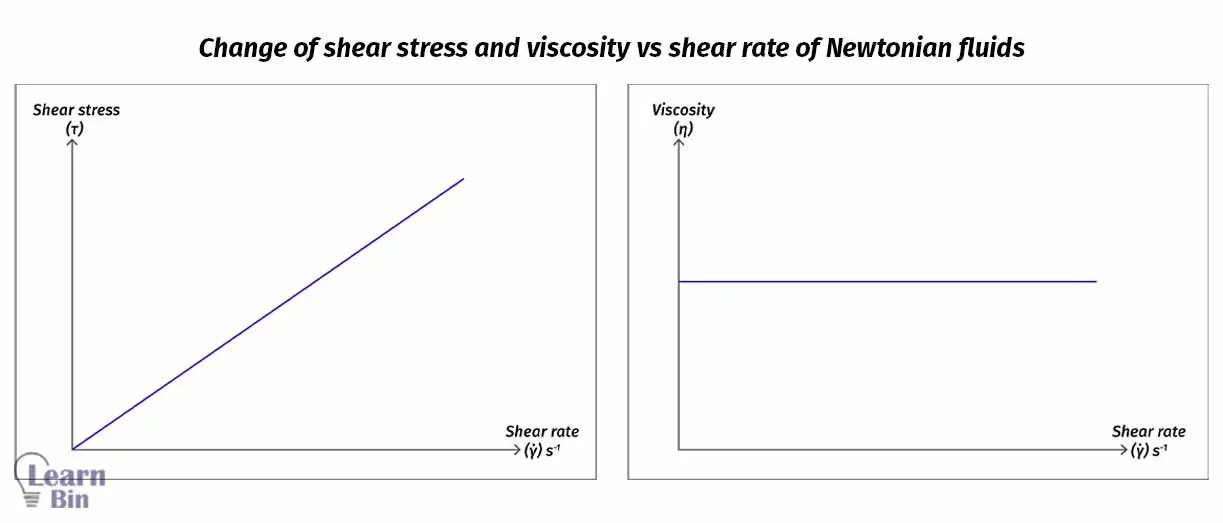
In Newtonian fluids, viscosity doesn’t change with the shear rate at a given temperature and pressure.
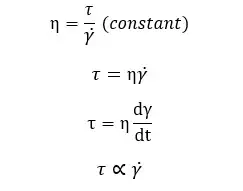
Where,
Some materials exhibit an infinite viscosity until sufficient stress is applied. Afterward, it starts to flow. Initial intermolecular interactions prevent the dispersion of materials until the limiting stress. If the external force exceeds the intermolecular interactions, the material will start to flow.
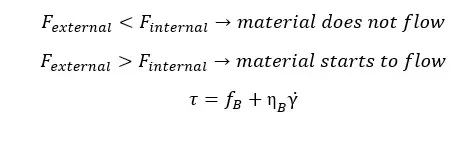
Where,
The yield point is the maximum shear stress at the shear rate at zero.
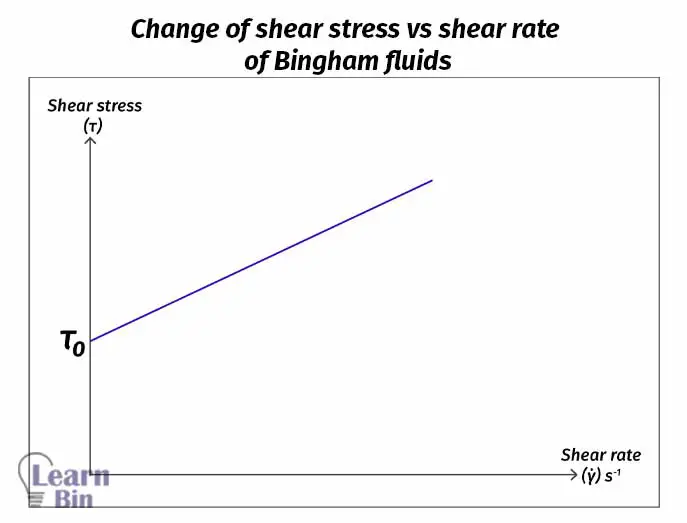
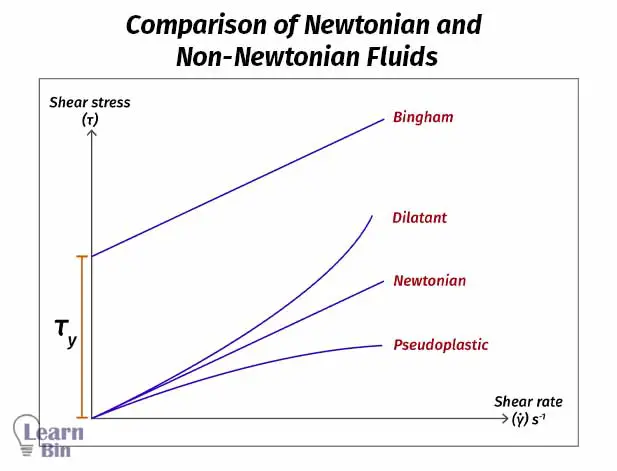
There are several mathematical models to describe the flow behavior of such fluids. Bingham model describes the flow behavior of Newtonian fluids having limiting stress.
Those are Newtonian and Non- Newtonian fluids. Non-Newtonian fluids change their viscosity or flow behavior under applied stress. Viscosity is either increased or decreased when shear is applied.
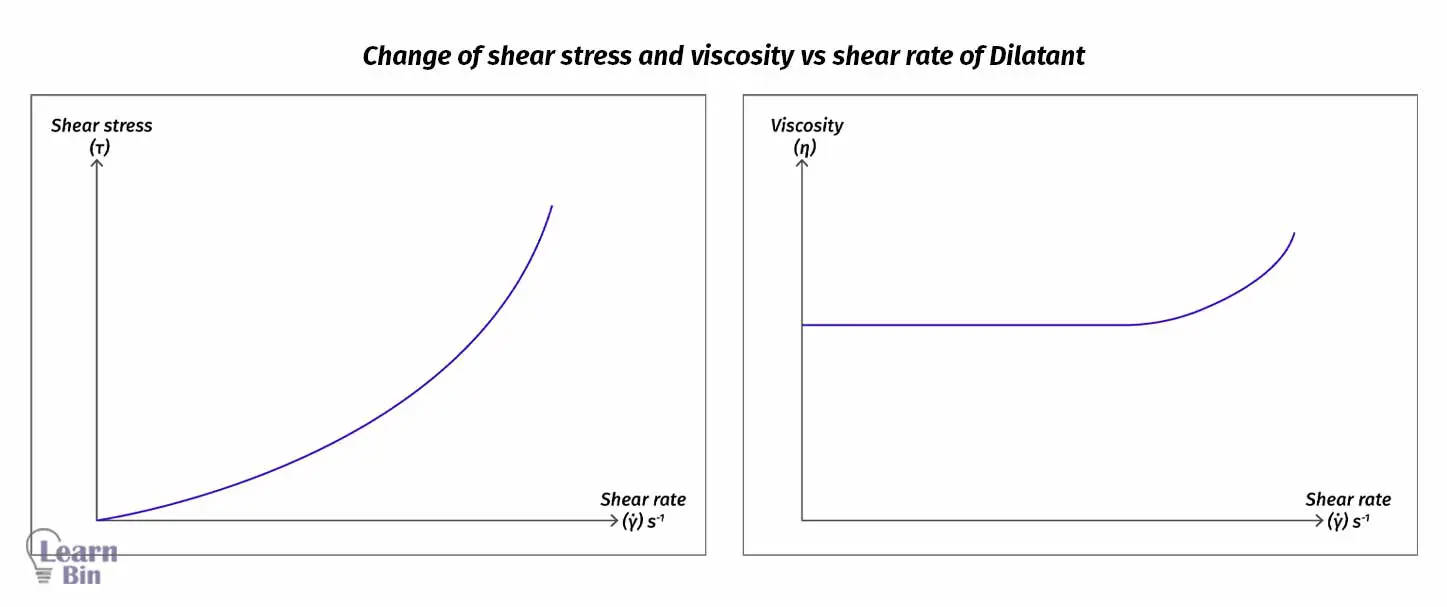
Some non-Newtonian fluids increase their viscosity and get thicker under shear stress. This is called shear thickening. Therefore, the fluid becomes less flowable and acts like a solid.
Some Non-Newtonian fluids decrease their viscosity under stress and become thinner fluids. This is known as shear thinning. Here the fluid becomes more flowable. These fluids come to their original viscosity when the stress is removed.
In many polymer materials (melts or liquids) viscosity of the medium decreases (shear thinning) with the increasing shear rates. So, these types of polymer melts require less energy to flow during the processing step. In such a system, we can only define the apparent viscosity where viscosity is changing as a function of the applying shear rate
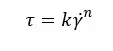
Where,
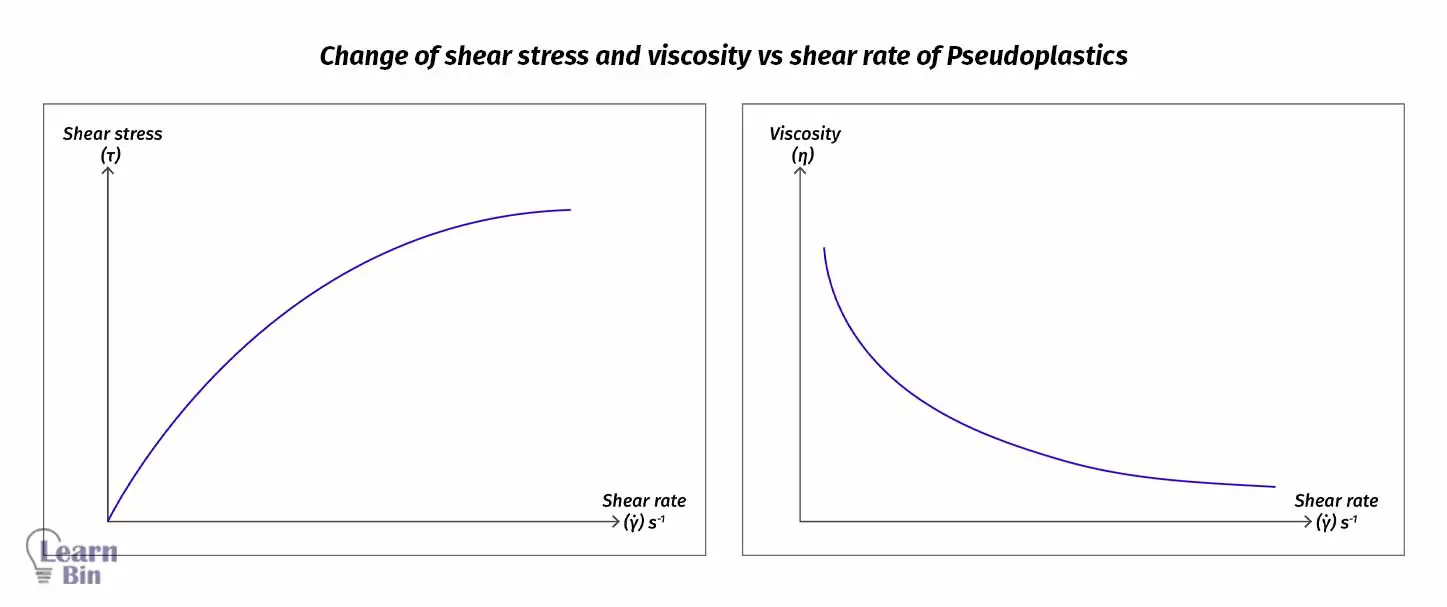
Dilatant materials increase their viscosity when applying shear stress (shear-thickening). This is a huge challenge in the polymer processing industry. Because dilatant materials need high energy to flow at a high shear rate. For dilatant materials, n is always higher than 1.
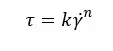
According to the Herschel and Bulkley model (Herschel-Bulkley model), both Newtonian and non-Newtonian fluids can be described. This describes the relationship between shear stress and the shear rate of fluids.
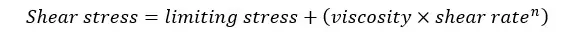
| Fluid | Limiting stress | n |
| Pure Newtonian fluid | 0 | 1 |
| Bingham fluids | >0 | 1 |
| Pseudoplastic | 0 | <1 |
| Dilatant | 0 | >1 |
This describes materials with power-law behavior at high shear rates. But it describes Newtonian behavior at low shear stresses.
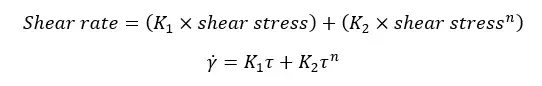
Where,
This model is used for materials that tend to Newtonian flow only at stresses much higher than the material yield stress.
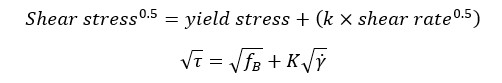
The viscosity of Newtonian fluids decreases with the increase in temperature, approximately in line with the Arrhenius relationship.
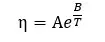
Except in some cases, viscosity decreases with the increase in temperature.
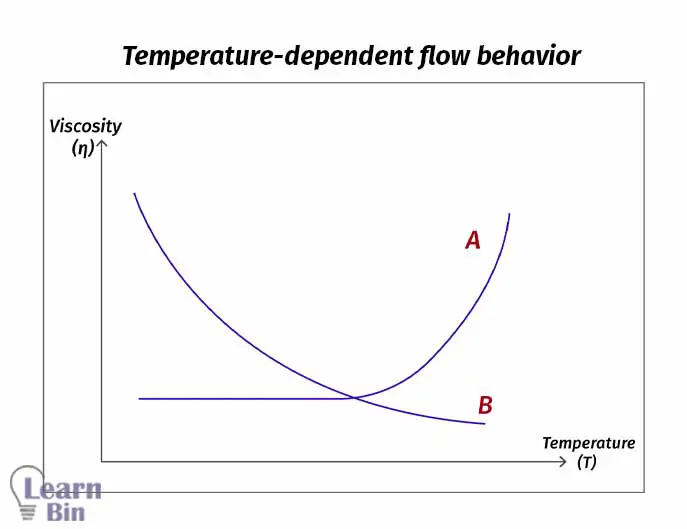
Polymer materials show time-dependent flow behavior where the time taken to stress accumulation and the time taken to stress release are different. There are two types of flow behaviors depending on the time.
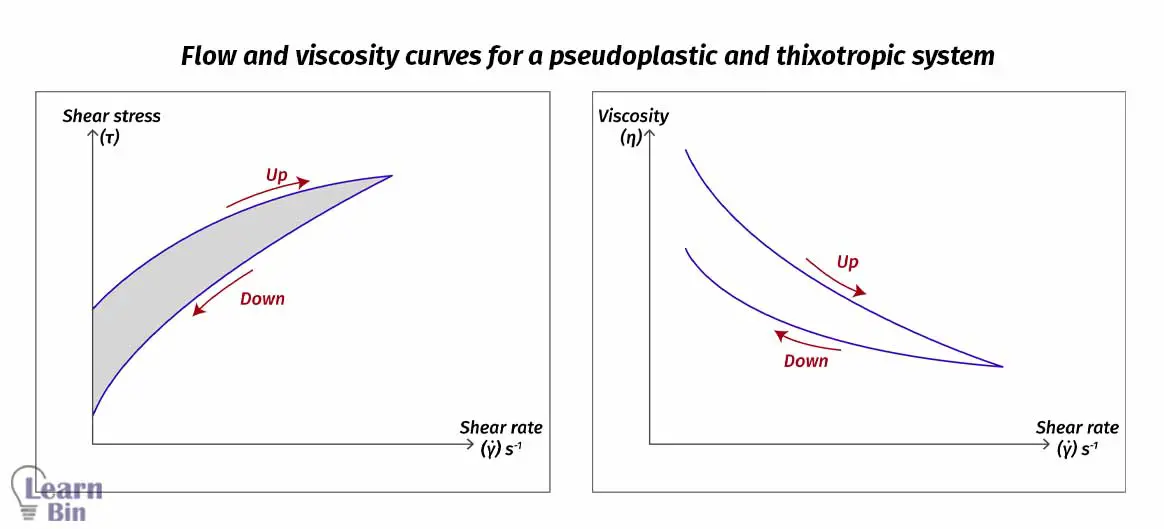
Thixotropic fluids take a longer time to stress relaxation. Therefore, restoring the viscosity to its original level takes a longer time. Thixotropic behavior is coupled with shear thinning behavior.
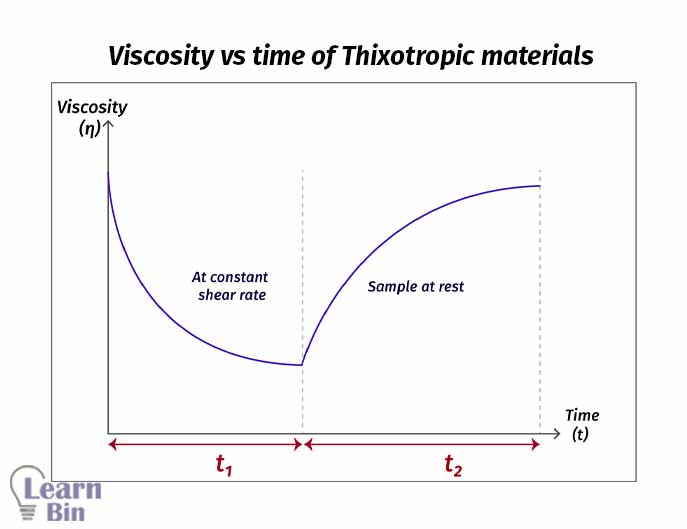
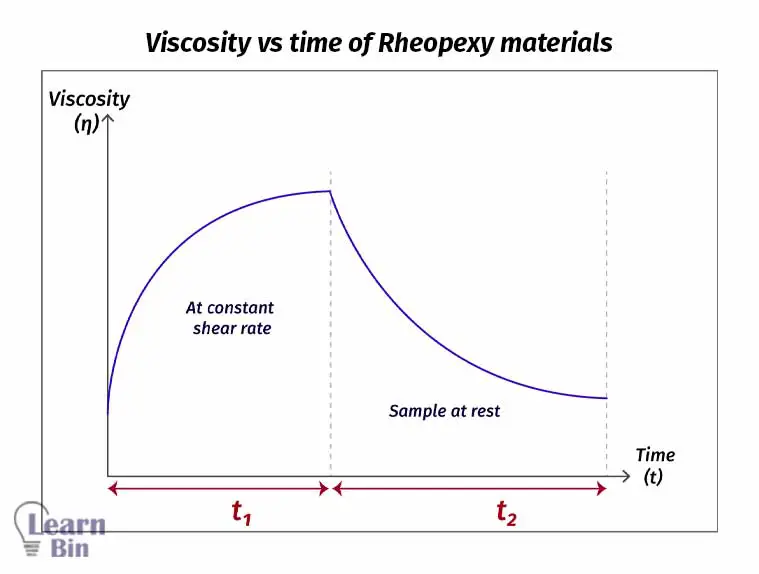
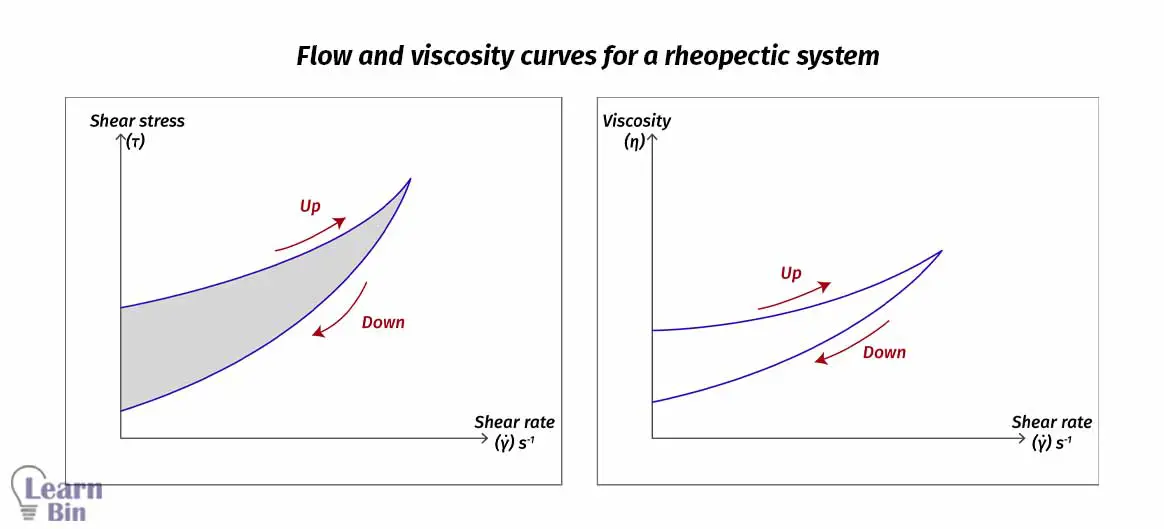
Rheopexy material shows the opposite time behavior compared to thixotropic polymer melts. Rheopexy is coupled with shear thickening behavior.
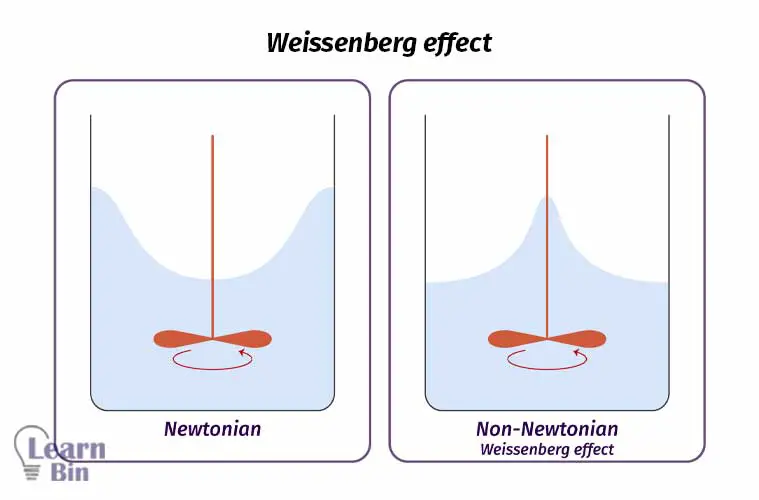
Weissenberg effect is used to identify Newtonian and non-Newtonian fluids. During this test, a propeller (impeller) is dipped inside the liquid or the melt. Newtonian liquids will be thrown outward from the propeller. The fluid body will arise along the propeller body in Newtonian fluids. This phenomenon is known as the Weissenberg effect.

The cover image was created using an image by PublicDomainPictures from Pixabay