Linear Motion

Motion is described as the change in position or the change in environment with respect to time. Any motion in the universe must be one of the following motions. If not, it must be a resultant movement of the following motions.

1. Linear motion
2. Angular motion
3. Simple harmonic motion

Linear motion or Rectilinear motion is the motion of an object along a straight line.

E.g –

• A fruit falling from a tree
• Motion of a vehicle on a straight road

Physical quantities related to the linear motion

Physical quantities that are related to linear motion are

• Distance,
• Linear displacement,
• Speed,
• Linear velocity,
• Linear acceleration,

and etc.

Distance (d)

The length of a path traveled by an object is called distance. The SI unit of distance is meters (m). Distance is a scalar.

Example 01

A ball is shot vertically upwards from the top of a building 80m high. The ball travels 10m vertically up and reaches the ground. Find the distance traveled by the ball.

Solution

Speed (V)

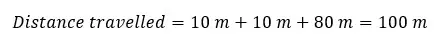
Speed is the rate of change in distance. If an object travels "S" distance within "t" time, the speed of the object can be written as follows.

Example 02

A vehicle is traveling at the speed of 108 kmh^-1.

1. Find the speed in meters per second (ms^-1)
2. Find the distance traveled at 10 seconds.
3. Find the time that takes to travel 1500m.

Solution

part 1

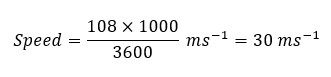
part 2

part 3

Example 03

Two objects A and B start to move at the same position in the same direction with the velocities of 4 ms^-1 and 6 ms^-1 respectively. Find the time taken for the distance between the two to be 30 m.

Solution

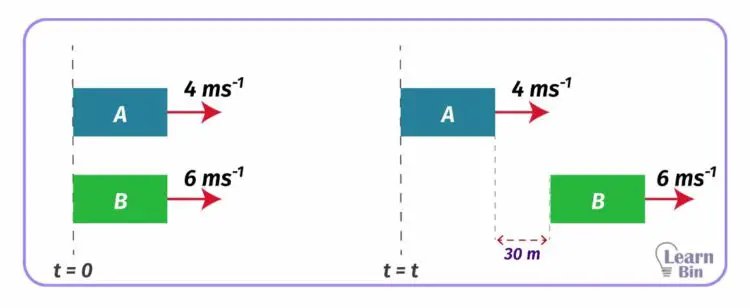
Let's take the time taken for the distance between A and B to be 30 m as "t". At the time "t" if object A, traveled distance x, object B has traveled x+30.

For object  A,

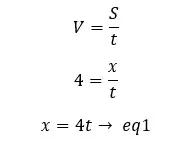
For object B,

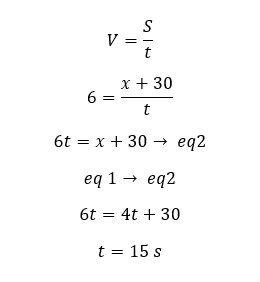
Example 04

A bat flies towards a wall 10m away with a speed of 20 ms^-1. The sound waves produced by the bat hit the wall and the bat hears an echo. If the speed of sound waves in air is 330 ms^-1, what is the distance between the bat and the wall when the echo is heard?

Solution

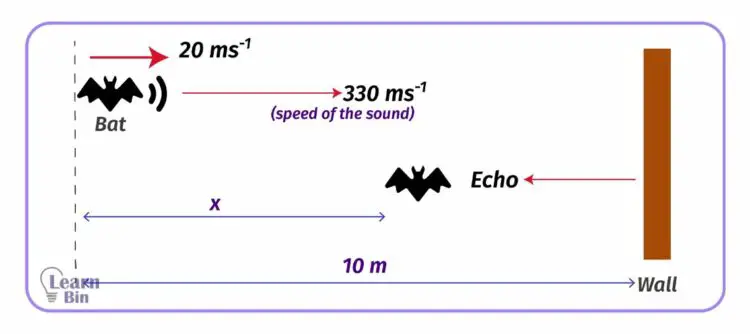
Let's take the distance traveled by the bat as "x" and the time is "t" when it hears the echo.

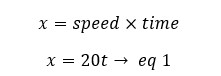
The distance should be traveled by the sound wave at the time "t",

Average speed

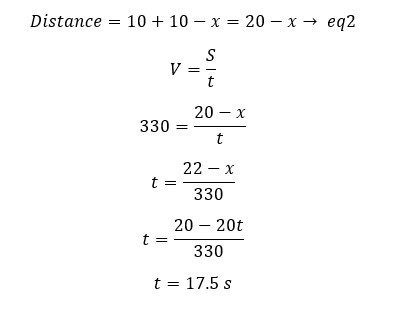
When an object changes its speed during the movement, we calculate the average speed for the entire movement.

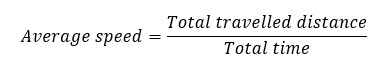
Example 05

A car traveling non-stop from city A to city B covers the first 200 km in 4 hours and the remaining 400 km in 5 hours. Find the average speed of the car.

Solution

Example 06

A bird flying up a hill travels 1.8 km in 9 seconds. The rest travel at a speed of 15 km h^-1 in five minutes. Find the average speed of the bird.

Solution

Example 07

A motorcycle travels from A to B. Half of the journey is at a speed of 50 km h^-1 and the other half at a speed of 30 km h^-1. Find the average speed of the motorcycle.

Solution

Let's take the total travel distance as "2x". Therefore, the halfway would be "x". Let's take the times taken to travel first half and second half are t₁ and t₂ respectively.

Linear displacement (d)

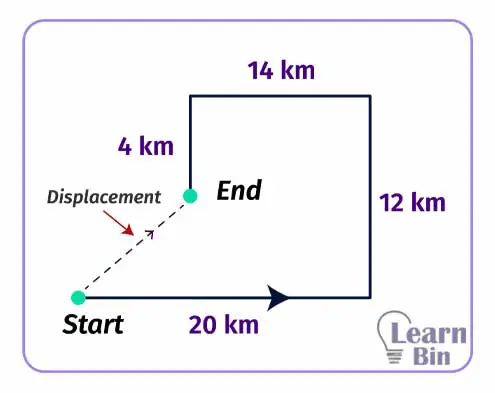
Displacement is the shortest distance between two points. Displacement is a vector.

Example 08

A car travels 20 km towards the east and then 12 km north. It again travels 14 km to the west and then travels 4 km to the south and stops. Find the displacement of the car.

Linear velocity (V)

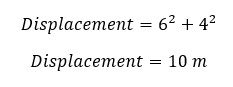
Linear velocity is the rate of the change of the linear displacement. Linear velocity is also a vector.

Average velocity

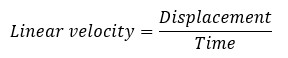
 If an object changes its velocity, we calculate the average velocity. If an object starts to move with the velocity of "U" and, after time "t" the object obtains a velocity "V" the average velocity can be written as follows.

Resultant velocity

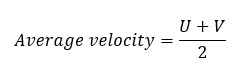
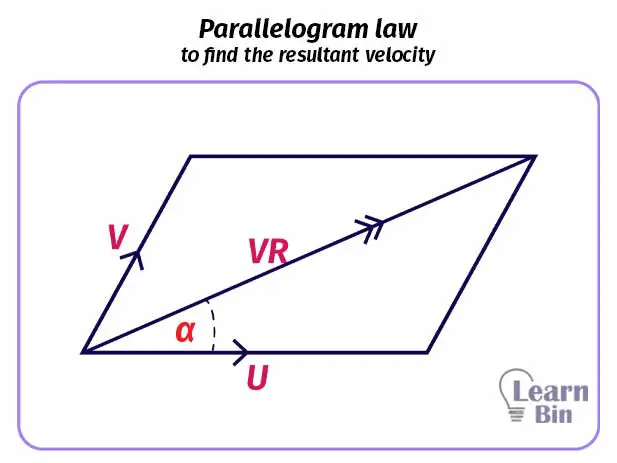
When an object has multiple velocities, we should calculate the resultant velocity. If two velocities act in the same direction, the resultant velocity would be the sum of the velocities. If two velocities act in opposite directions, the resultant velocity would be the difference in velocities. If there is another angle between velocities, we can use the parallelogram law to find the resultant velocity

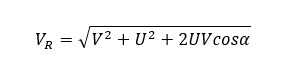
Example 09

A train is moving at a speed of 240 km h^-1 on a straight railway track. Find the displacement taken at 5 minutes. What is the time taken to travel 1200 km at this speed?

Solution

Time taken to travel 1200 km,

Example 10

When two cars (A and B) move in the same direction, they approach each other by 4 meters in 1 second. When the two cars move in opposite directions, they move away from each other by 2m in 1 second.

Solution

Let's take the velocities of A and B are V_A and V_B.

Linear acceleration (a)

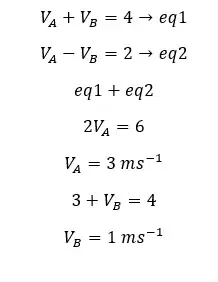
Linear acceleration is the rate of change of velocity of an object that is in a linear motion. If the acceleration is decreasing with time, it is a negative acceleration. Negative acceleration is commonly known as "Retardation" or "De-acceleration". Linear acceleration is a vector. If an object starts a linear motion with a velocity of "V" and after time "t" it obtains velocity "V", the acceleration can be written as follows,

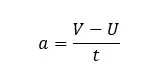
Example 11

An object moving on a straight line takes 10 seconds to obtain 60 ms^-1 velocity from 10 ms^-1 velocity. Find the linear acceleration, Average velocity, and Displacement of the object.

Solution

Linear acceleration

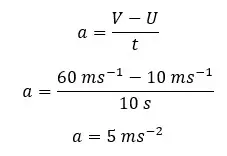
Average velocity,

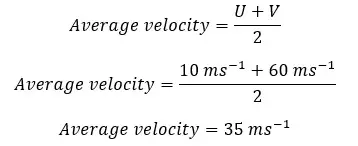
Linear displacement,

Example 12

An object with an acceleration of 8 ms^-1 acquires a velocity of 40 ms^-1 in 4 seconds. Find the initial velocity, Average velocity, and Displacement of the object within 4 seconds.

Solution

Initial velocity,

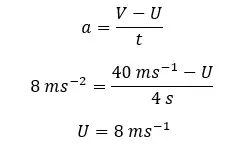
Average velocity,

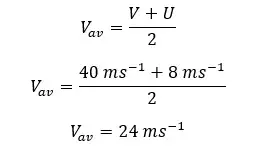
Displacement within 4 seconds,

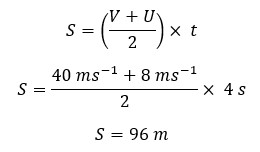
Example 13

The velocity of a bullet that travels toward a wooden block is 220 ms-1.  After the bullet hits the wood, it sinks into the wood and decreases its velocity to 20 ms^-1 within 0.2 seconds. Find the de-acceleration and the displacement taken place by the bullet at 0.2 seconds.

Solution

De-acceleration

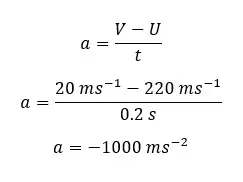
Displacement

Motion equations

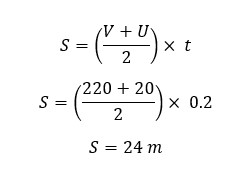
We can use the following equations to solve problems associated with motion. But these equations are only valid for linear motion and if there is an acceleration, it should be constant.

Where,

• S = Linear displacement
• U = Initial velocity
• V = Final velocity
• a = Linear acceleration
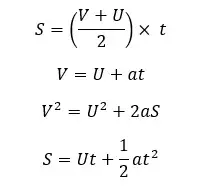
• t = Time

Next learn about another important concept of mechanics, Linear momentum.