More results...


In previous articles, we discussed the thermal expansion of matter, linear expansion of solids, and area expansion of solids. In this article, we discuss how temperature changes in a solid object would affect its volume.
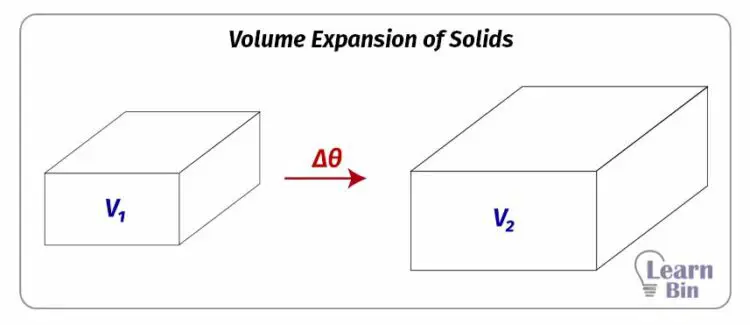
Volume expansion of solids is the increase in an object's volume when the temperature increases.
The expansion of volume is proportional to its initial volume and the temperature difference. If the volume of an object is increased from V1 to V2 when the temperature is increased by Δθ, mathematically,
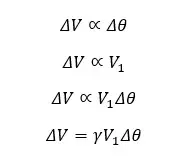
Where,
Since ΔV is V2 - V1, the final volume of the object is expressed as follows,
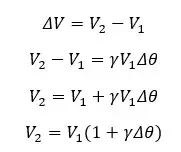
The volume expansion coefficient is a proportional coefficient that depends on the type of the material. If the material is thermally isotropic, the volume expansion coefficient can be expressed in terms of the linear expansion coefficient.
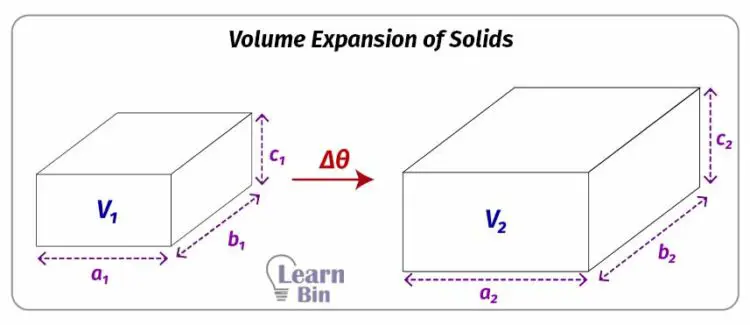
If the linear expansion coefficient of the material is α, the linear expansion of each side of the above cube would be,
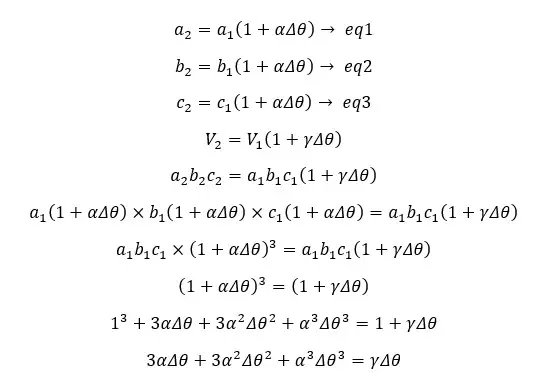
The volume expansion coefficient is around 10-5 °C-1. Therefore, α2 and α3 are negligible when compared to α. Therefore, the equation can be rewritten as follows.
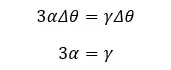
Question 01
An Aluminum cube with a volume of 4m3 is heated to 500 °C. Find the final volume of the aluminum cube. The volume expansion coefficient of aluminum is 6.9 ×10-5 °C-1.
Solution
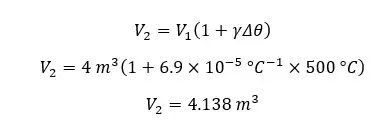
Question 2
A glass ball with a thermal expansion coefficient of γg and a Volume of Vg has been inserted into a cylinder. Then the cylinder is heated by Δθ. If the interspace volume between the cylinder and the glass ball does not change even after heating, express the thermal expansion coefficient of the cylinder in terms of the thermal expansion coefficient of glass.
Solution
In order not to change the interspace volume after heating, the expansion of the glass ball must be equal to the expansion of the cylinder. If the initial volume of the cylinder is Vc and the thermal expansion coefficient is γc,
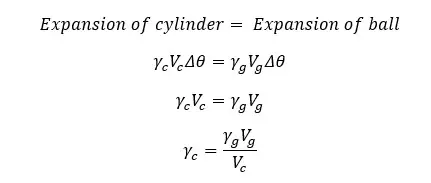

The cover image was created using an image from PxHere, licensed under CC0 Public Domain