More results...


The work done in bringing a positive charge of +1C at infinity to a point in an electric field is called the electric potential of that point.
If the work is done by the electric field, the electric potential of the point is negative. If the work is done on the electric field, the electric potential is positive. If there is no work done, the electric potential is zero.
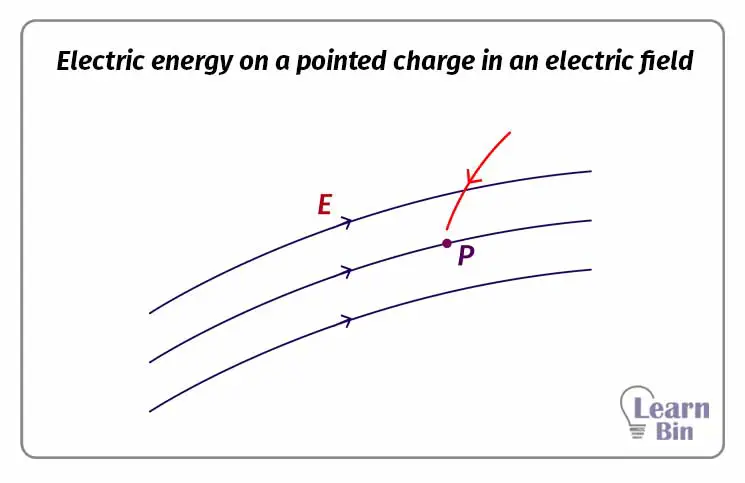
Let's imagine a pointed charge of +1C (+q) is brought to a point P, which is in an electric field, from infinity.
If the work done on the field is W, mathematically,
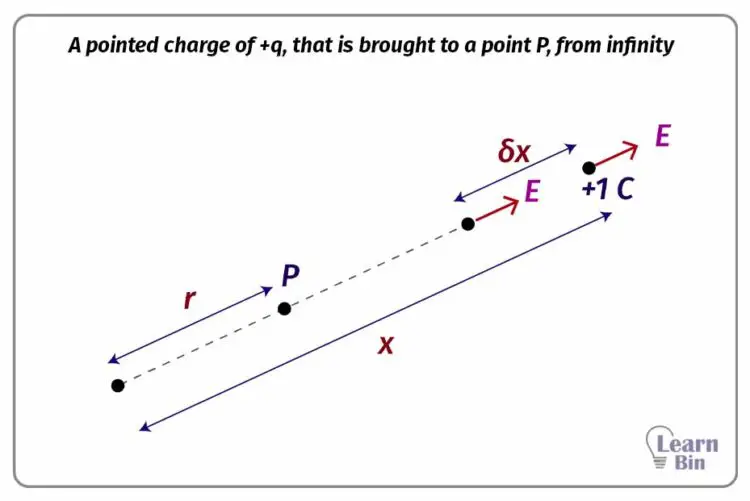
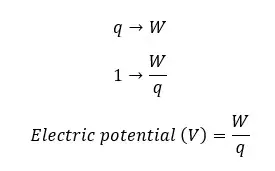
Consider there is a pointed charge of +Q in an electric field. Let's find the electric potential of a point "P" which is in "r" distance from the pointed charge. The electric field intensity of a point which is in "x" distance from the pointed charge is "E", and if the work done by the electric field when a +1C charge is carried to dx distance is dV, mathematically,
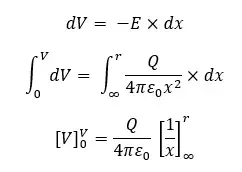
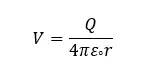
Question 01
What is the electric potential of a point that is 9 cm far from a pointed charge of +2μC?
Solution
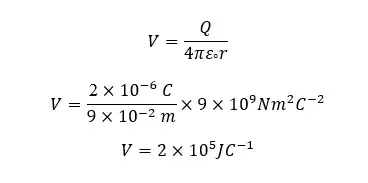
Question 02
Find the electric potential of point P, due to the following pointed charges.
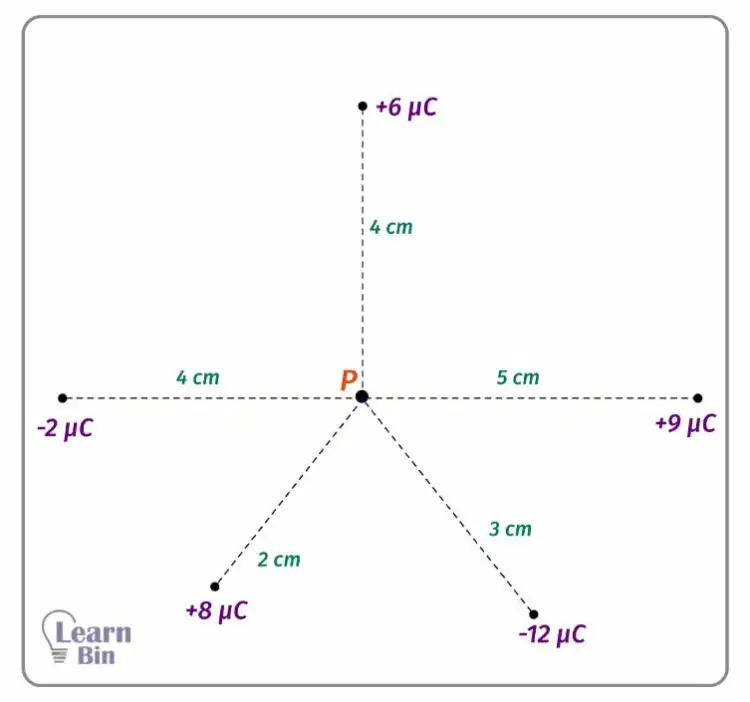
Solution
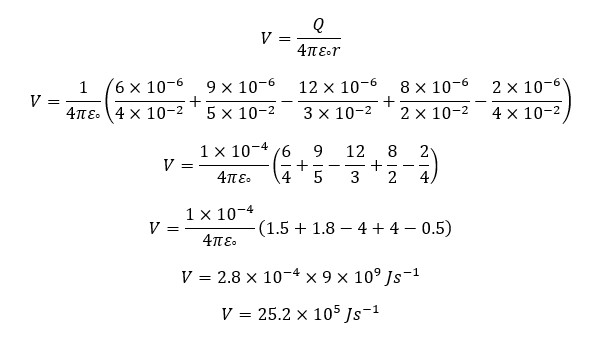
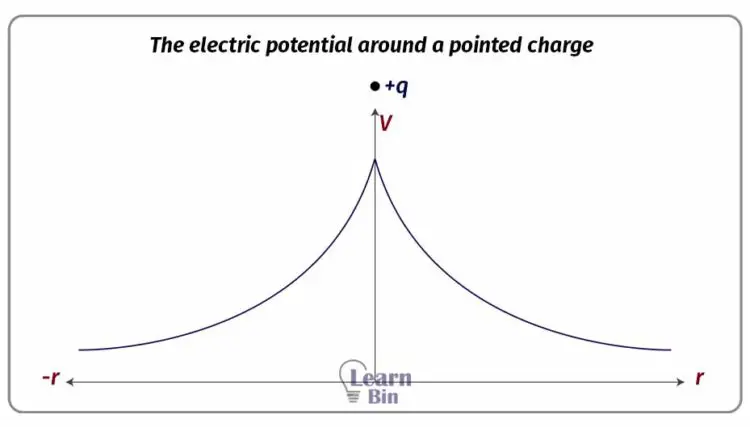
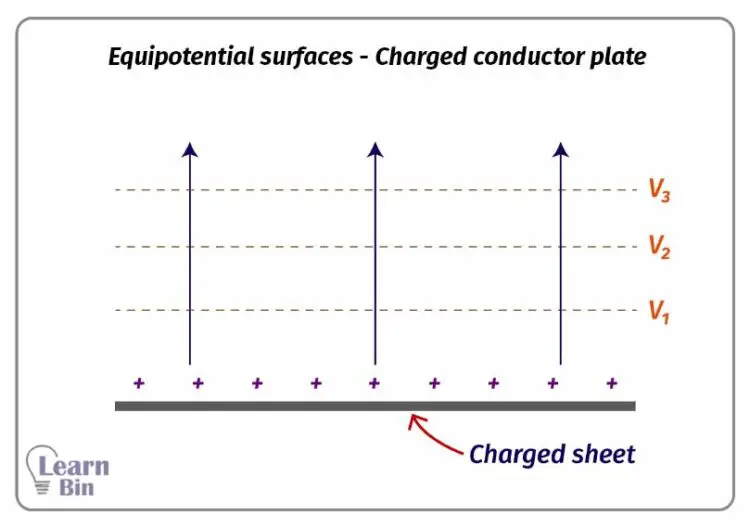
An equipotential surface is where each point of the surface has the same electric potential. An equipotential surface is defined as the geometrical shape obtained when points of equal potential are joined. The equipotential surface is always perpendicular to the electric field lines.
E.g., Charged conductor plate
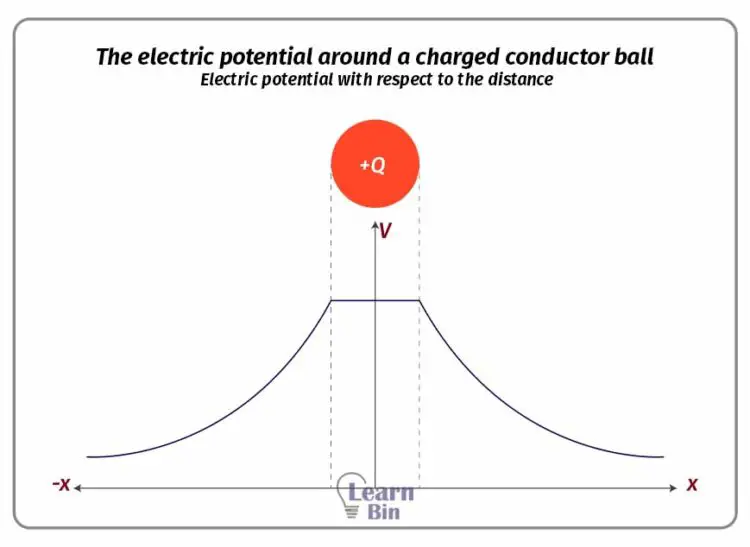
To find the electric potential around a charged conductor ball, let's assume three points of A, B, and C which are outside the ball, on the ball, and in the ball respectively,
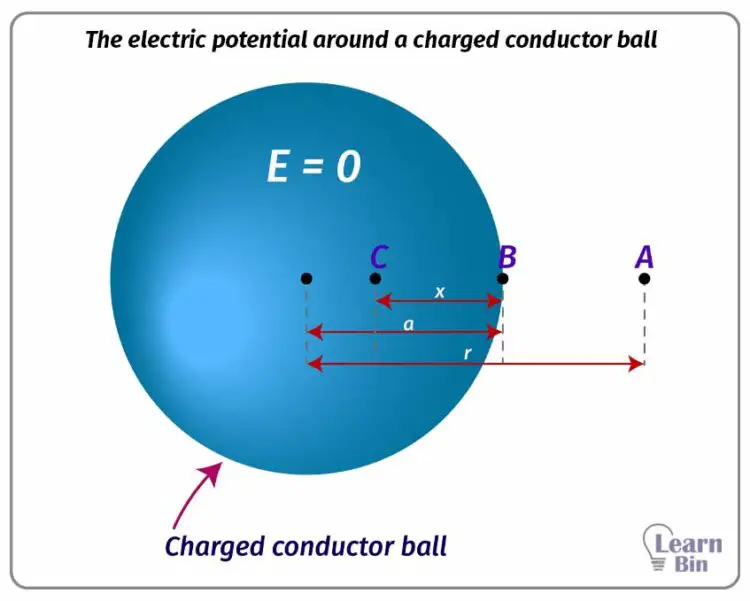
The electric potential of each point is as follows,
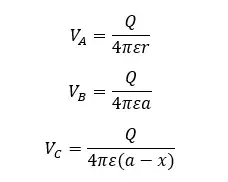
Electric field intensity at point C,
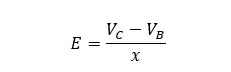
The electric field intensity inside a conductor ball is zero. Therefore,
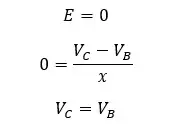
This equation shows that there is the same electric potential inside a conductor ball, even though the electric field intensity is zero. There is always the same potential inside a conductor ball, no matter whether it is a hollow or solid ball. The charge of electric potential with respect to the distance can be represented as follows.
The electric potential of a point in an electric field is the energy that is taken by a pointed charge with +1C which is in that point. Therefore, electric energy which is taken by a pointed charge with +Q charge would be,
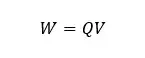
When a pointed charge of q is placed with r distance from another pointed charge of Q, the electric energy of the "q" charge would be,
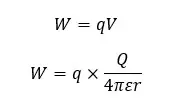
Question 03
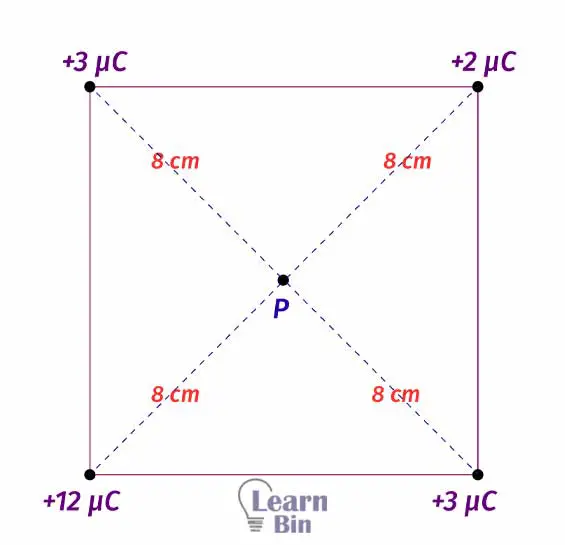
Four pointed charges are placed on each vertices of a square. Find the electric field intensity and the electric potential of the point P, where the diagonals of the square intersect. The distance between point P and the vertices of the square is 8cm.
Solution
Equal charges have been placed on opposite vertices of the square. Therefore, the electric field intensity due to the charges would be canceled out. The electric field intensity of point P is zero.
Electric potential,
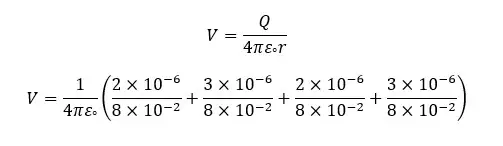
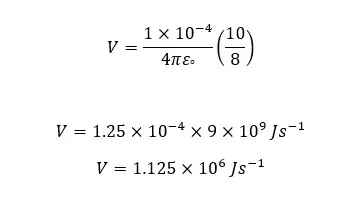

The cover image was created using an image by OpenClipart-Vectors from Pixabay