What is the Miller Index?

Miller index is a notation system that describes the size and the direction of planes of atoms/crystal plane in a crystal. Miller indices of a crystal plane are denoted by three numbers which are usually indicated as hkl values.

Planes of atoms / Crystal plane

Crystalline materials are materials that have periodically and orderly arranged molecules or atoms. The basic repeating unit of a crystal is known as the unit cell.

The imaginary planes that intersect the atoms in a crystal are known as crystal planes or planes of atoms. These planes can be used to define the direction and the distance between the atoms in the unit cell.

How to find the Miller Index?

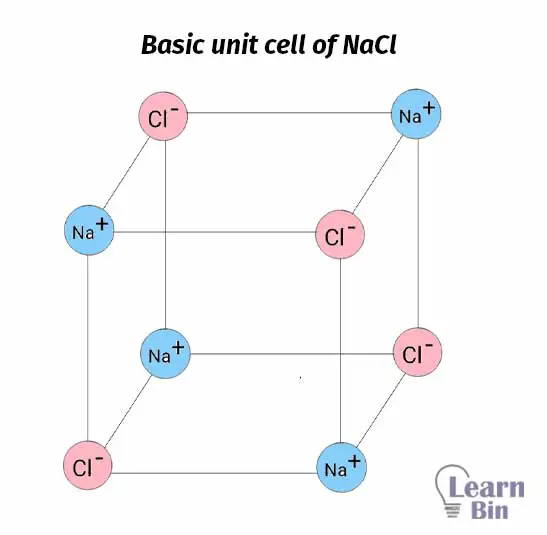
Consider a cubic unit cell with particles (atoms) at each corner. Then, select any plane of atoms, that intersect atoms in the unit cell.

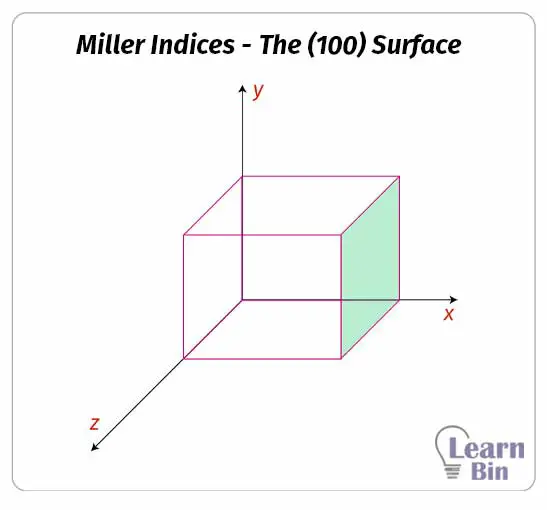
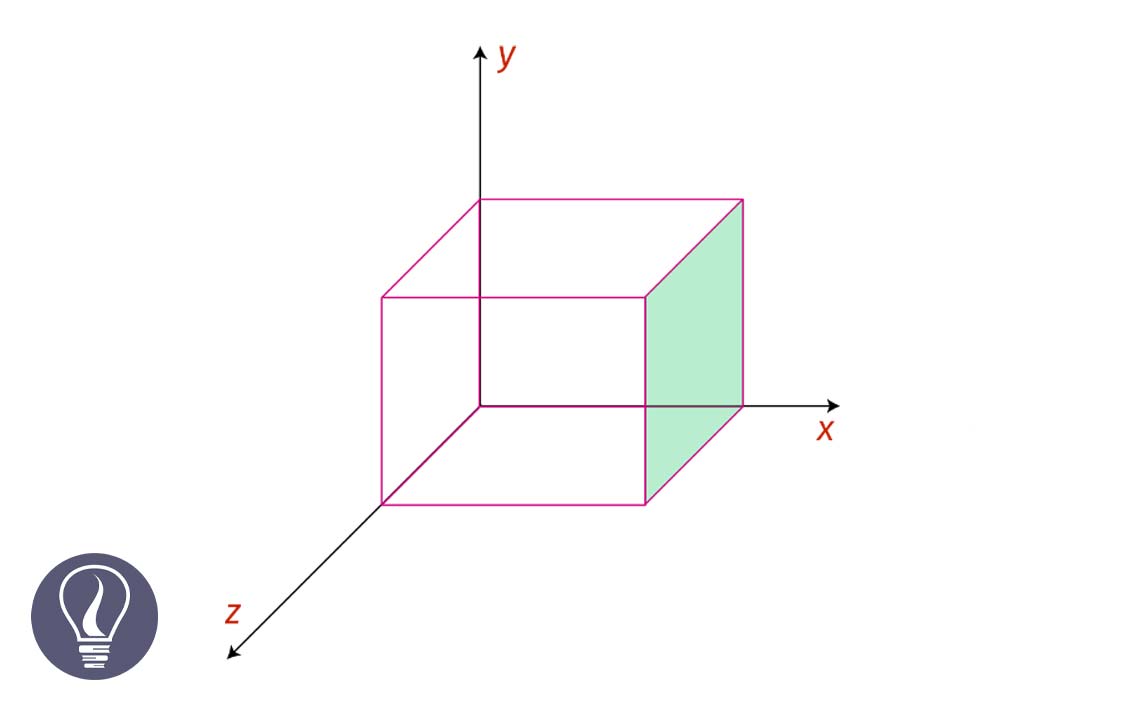
Take the x, y, and z coordinates of that selected plane. The above plane intersects the x-axis at 1, therefore, the x-coordinate of this plane is 1. This plane does not intersect both the y and z axes.

Therefore, the y and z coordinates of this plane are infinity.  (x =1, y = ∞, z = ∞) To convert these coordinates to Miller indices, take the reciprocal of each value. After taking the reciprocal, it will indicate as (hkl) values respectively.

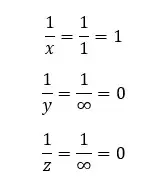
Miller index of the above plane is (100). We do not use commas in separating values in the Miller index.

Now, let's find the miller index of the following plane, which has intercepts of x, y, and z are 2, 1, and 3 respectively.

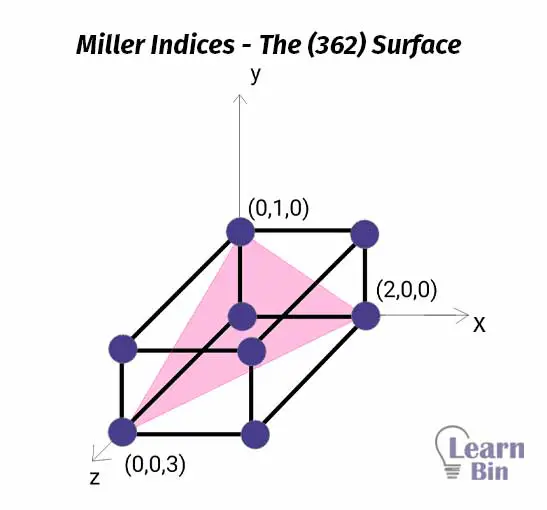
First, we need to take the reciprocal of each value.

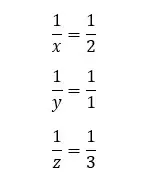
However, the Miller index cannot be a fractional value. Therefore, the numbers should be multiplied by the Least common multiple (LCM) of the three denominators. LCM of 2,3, and 1 is 6.

Therefore,

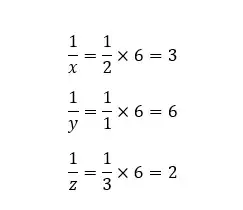
The miller index of the above plane is (362).

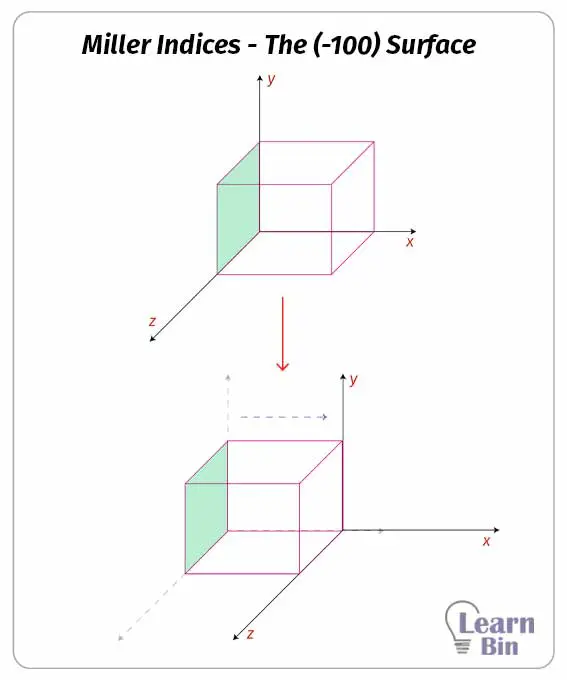
Consider the crystal plane passing through the origin as shown in figure 4. In this situation, the intercept of x is 0. To convert this into the Miller index, the reciprocal of zero should be taken. But the reciprocal of zero is undefined. Therefore, we move the origin to the nearest lattice point.

After moving the origin, the new intercepts of x, y, and z are -1, ∞, ∞ respectively. After converting x, y, and z values to the Miller indices, it would be (-100). This is usually represented as (-100)

Experimental way to find the Miller index

To find the Miller index experimentally, a principle known as Bragg's law can be used. For this equipment that is based on this principle such as the powder diffractometer can be used. We will discuss them in separate articles.