More results...
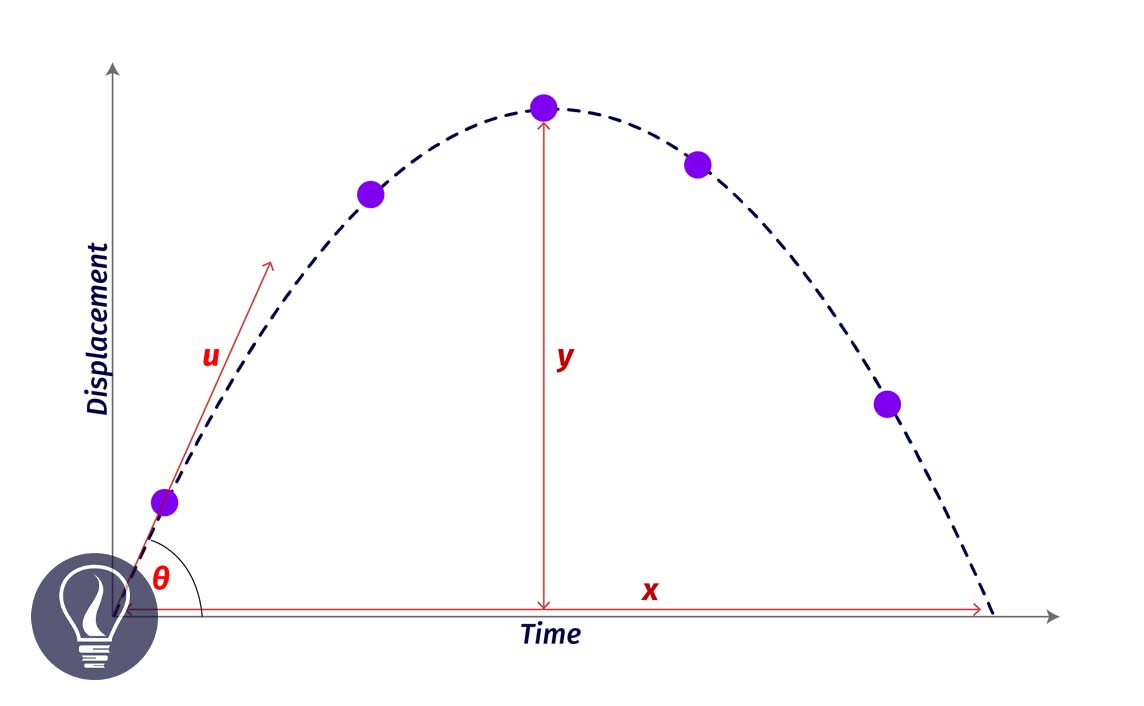

Projectile motion is a motion of an object that is moving inclined to a gravitational field and it is not affected by air resistance. Projectile motion is a resultant motion of two linear motions, which are vertical and horizontal motions. The path of an object of a projectile motion is a trajectory.
E.g.
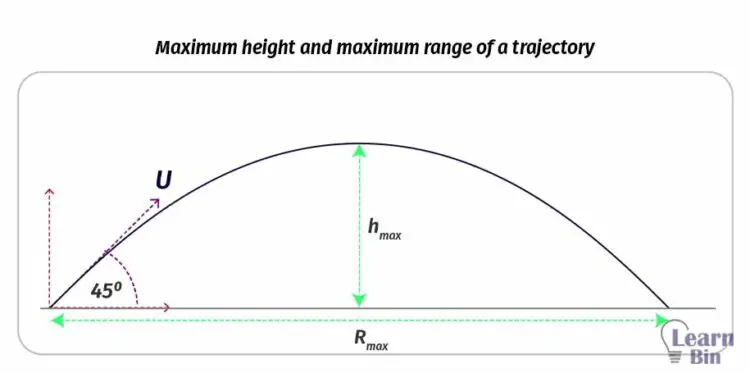
Let's assume that an object is projected, with a “θ” angle to the horizontal axis and "U" initial velocity. The object will travel in a trajectory as shown in figure 02.
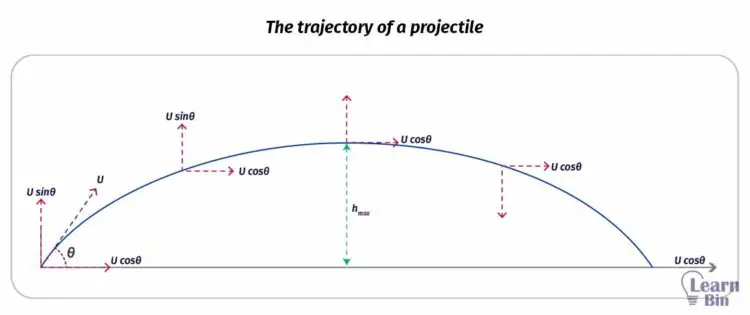
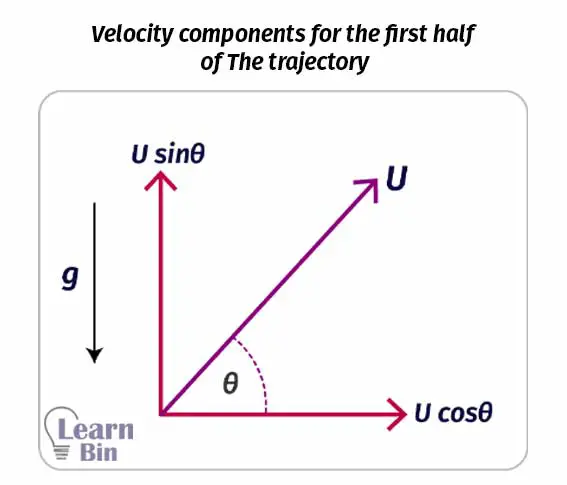
Since the object is projected “θ” angle to the horizontal axis, the initial horizontal velocity component would be “U.cosθ”. This velocity does not change during the entire motion. The initial vertical velocity component would be “U.sinθ”. This value is gradually decreasing until the object reaches its maximum height.
At the maximum height, the vertical velocity component is zero. After it obtains the maximum height, it comes down through a trajectory.
The vertical velocity decreases until it reaches the maximum height because there is an opposite force acting on the vertical component of the velocity. The opposite force is the gravitational force.
Therefore, the object is de-accelerating. When it is coming back to the ground, the gravitational force acts in the same direction as the vertical component of the velocity does. So, the object is accelerating.
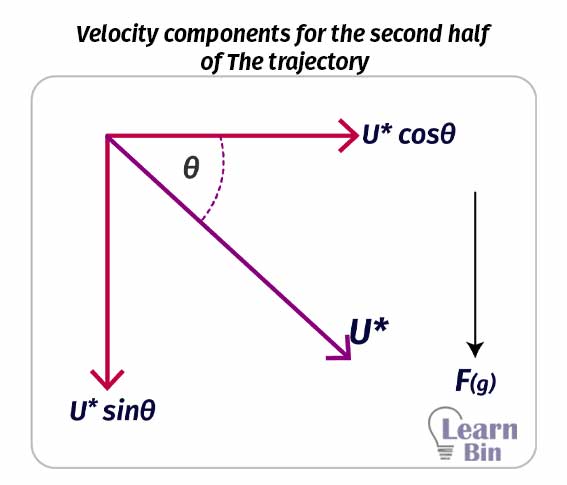
Using motion equations, we can find the maximum height, maximum range, and flight time of the object.
At the maximum height, the velocity is zero. The object is subjected to a negative acceleration due to the opposite gravitational force. If the maximum height is “h” we can obtain an equation for the maximum height as follows.
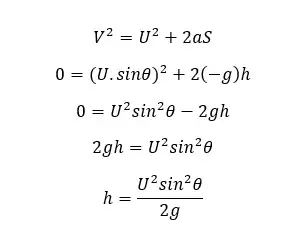
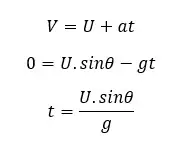
To find the flight time of the object we can apply a motion equation for the vertical direction of the motion. Since the object comes back to the ground, the vertical displacement of the object is zero. (S = 0). The gravitational acceleration affects the opposite direction of the object.
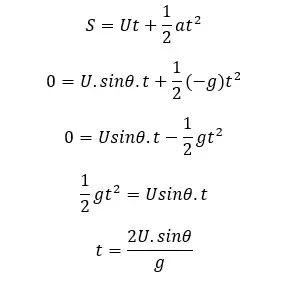
To find the flight range we apply a motion equation for the horizontal direction. There is no effect of gravitational acceleration on the horizontal velocity component. Therefore, the horizontal velocity component is a constant.
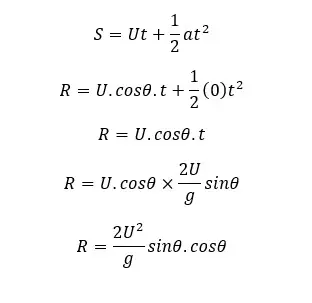
To get a maximum height and a maximum range, the object should be projected at a 45° angle to the horizontal axis.
Maximum range
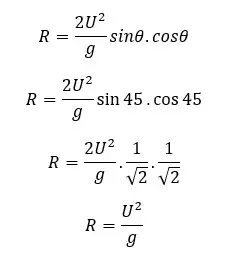
Maximum height
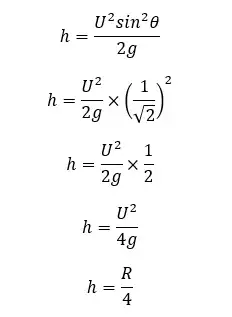
The above equation shows that the maximum height would be ¼ of the maximum range when the object is projected at a 45° angle to the horizontal axis.
Question 01
An object is projected at a 30° angle to the horizontal axis at 60 ms-2 initial velocity. Gravitational acceleration is 9.81 ms-2. By assuming that there is no air resistance involved, find,
Solution
1. The initial horizontal velocity component

2. Initial vertical velocity component

3. Maximum height
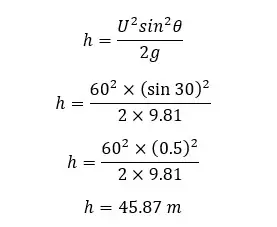
4. Time taken to reach the maximum height
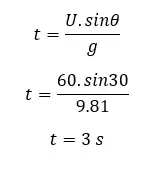
5. Horizontal range
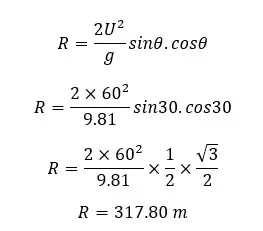
Question 02
A bullet is projected to obtain a maximum height and maximum range. The bullet obtains 1200 m of maximum range. Find the maximum height, initial velocity, and flight time of the bullet.
Solution
Maximum height
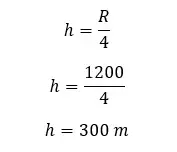
Initial velocity
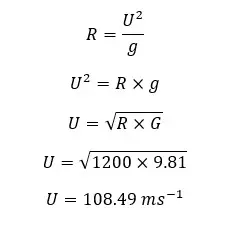
Flight time of the bullet
Since the bullet reaches its maximum range and maximum height, we can assume that the bullet has been projected at a 45° angle to the horizontal axis.
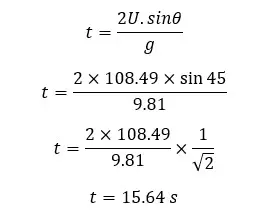
Question 03
A ball is projected at the top of a tower 65 m in height. The angle that the ball projected is 30° to the horizontal axis. The initial velocity of the ball is 24 ms-1. Find the flight time of the ball and the velocity when it hits the ground.
Solution

We can divide the overall path of the ball into two sections as shown in figure 6.
The time taken to reach the maximum height
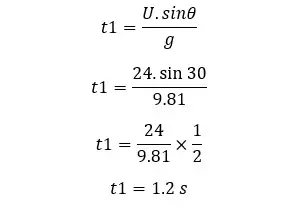
After 1.2 seconds, the ball reaches the maximum height of the trajectory. At the maximum height, the vertical velocity component would be zero. The total displacement that the ball will take until it hits the ground is a maximum height of +65 m. So, first, we should find the maximum height of the trajectory.

Now we can apply a motion equation to the vertical direction to find t2. The initial vertical velocity component is zero and the gravitational acceleration acts in the same direction of the object travels.
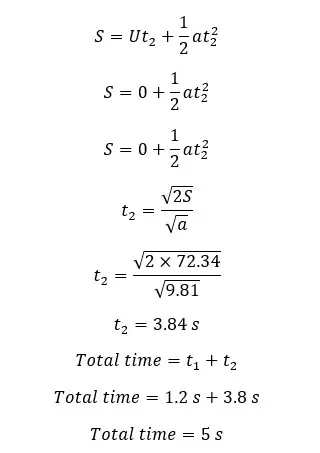

The cover image was designed using an image by Maxmath12, licensed under CC0, via Wikimedia Commons