Band-Pass Filters (BPF) - Active Band Pass Filter and Passive Band Pass Filter

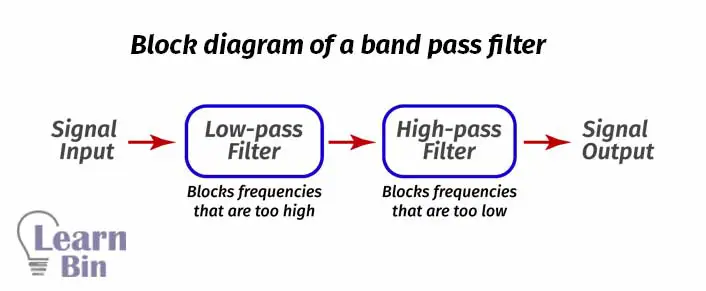
A band-pass filter is an electronic filter that passes all signals lying within a band between a lower-frequency limit and an upper-frequency limit. So, the band pass filter (BPF) will reject all other frequencies that are outside the specified band. The band-pass filter is a combination of a high pass filter and a low pass filter.

Active band pass filter

Calculation of the transfer function of an active band-pass filter

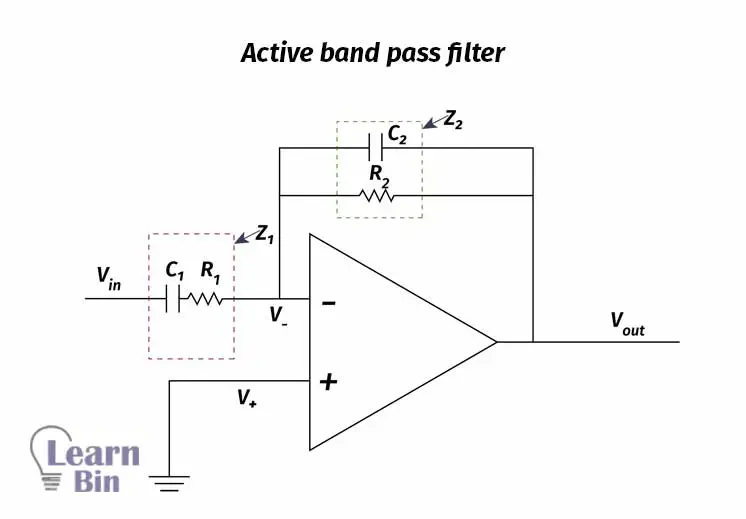
Where V_in is the input voltage and V_o is the output voltage, the voltage gain of an active band pass filter can be written as follows,

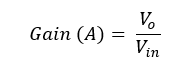
V_in is affected by the impedance given by both the R₁ resistor and C₁ capacitor. The total impedance can be written as follows,

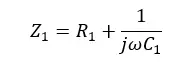
According to the Kirchhoff law, V_in will be,

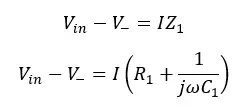
Where V+ has been grounded, V- also be zero. Therefore,

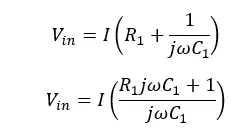
V_out is affected by the impedance given by both the R₂ resistor and the C₂ capacitor. The total impedance can be shown in the following equation,

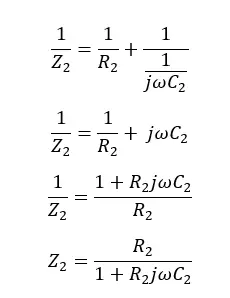
Output voltage V_o is given by,

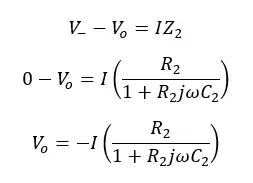
Where,

• V_in = Input voltage
• V_o = Output voltage
• R₁ = Resistance of the R₁ resistor
• R₂ = Resistance of the R₂ resistor
• C₁ = Capacitance of the C₁ capacitor
• C₂ = Capacitance of the C₁ capacitor
• Z₁ = Impedance given by R₁ resistor and C₁ capacitor
• Z₂ = Impedance given by R₂ resistor and C₂ capacitor

Therefore, the voltage gain will be,

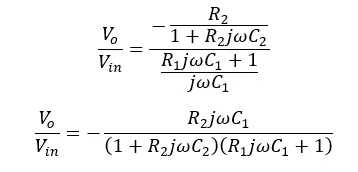
Let's take,

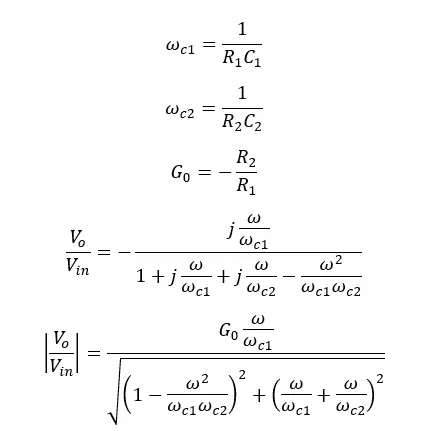
The above equation is the transfer function of an active band pass filter.

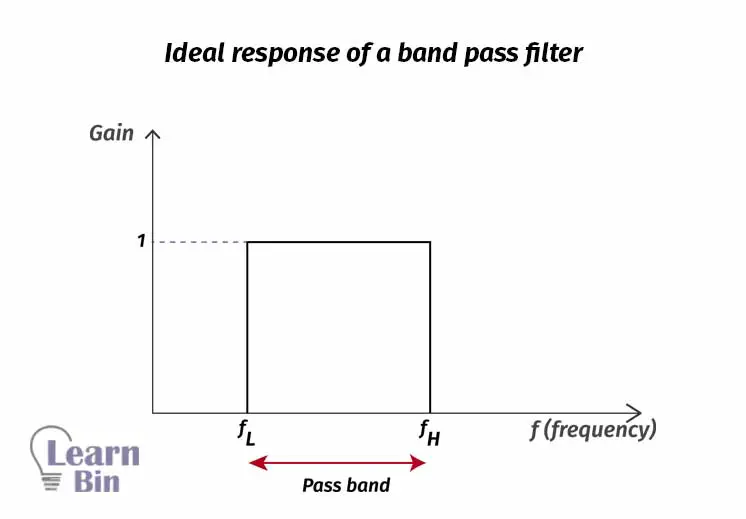
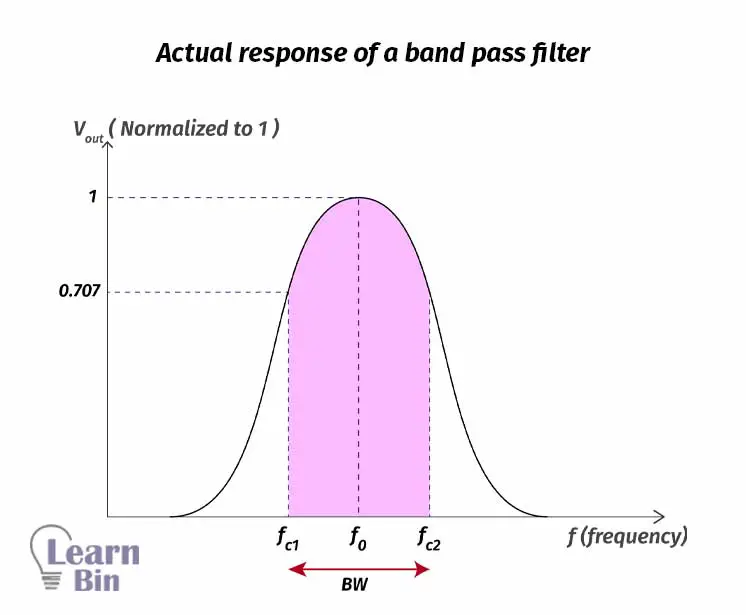
The difference between the upper critical frequency (f_c2) and the lower critical frequency (f_c1) is identified as The bandwidth (BW). Upper critical frequency f_c2, lower critical frequency f_c1, and bandwidth can be calculated as follows.

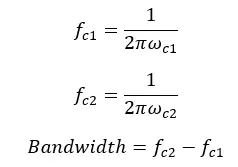
The frequency that the pass band is centered is known as the center frequency, f_o. Center Frequency can be defined as the geometric mean of the critical frequencies. The center frequency is calculated as follows.

Passive band pass filter

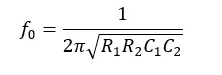
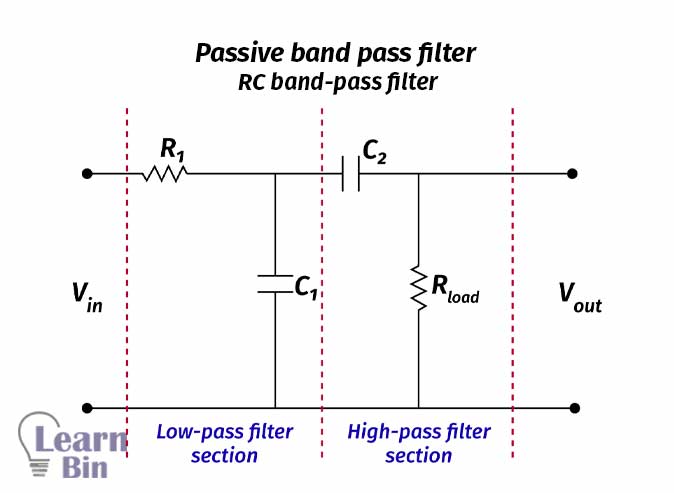
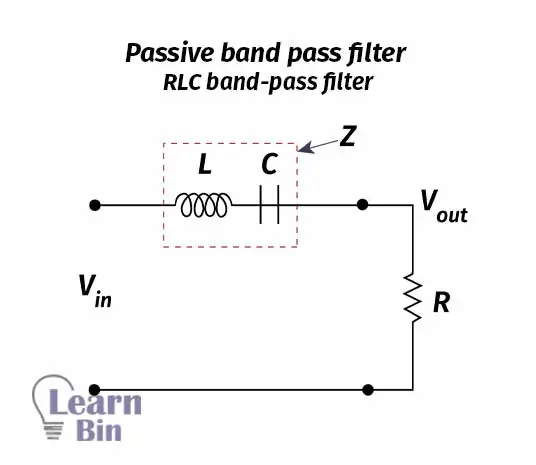
Passive band pass filters can be either RC circuits or RLC circuits

Calculation of the transfer function of an RLC band pass filter

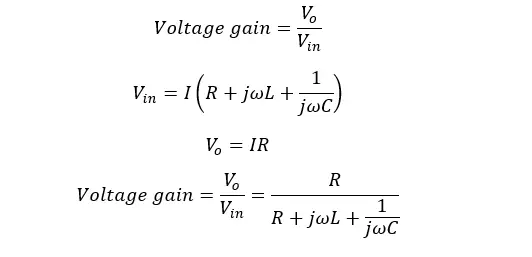
Where,

• R = resistance of the R resistor
• ω = Angular frequency of the signal
• C = capacitance of the C capacitor
• L = inductance of the L inductor

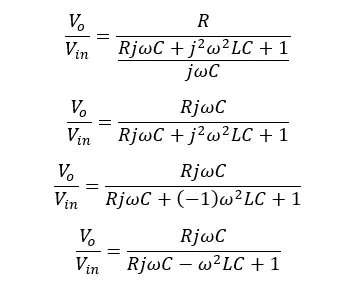
For ease of simplification, let’s take the reciprocal of the voltage gain,

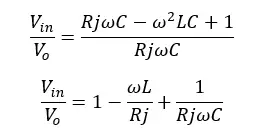
To remove the complex parts of the equation, the 4^th power of complex parts is taken separately and the 4^th root is taken. So, the transfer function is given by,

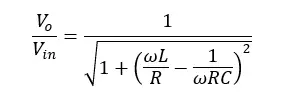
When ω = ω₀ (angular frequency at the center frequency, f₀), voltage gain shows the highest value which is 1. At the highest gain,

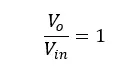
To fulfill the above requirement, at the center frequency,

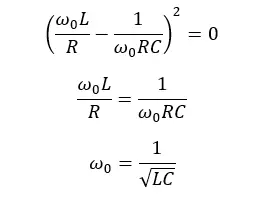
For the 3dB cutoff frequency,

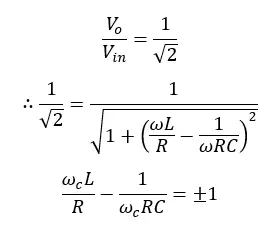
By solving the above equation, upper and lower 3dB frequencies can be obtained.

• Lower critical frequency,

• Upper critical frequency,

• Center frequency,

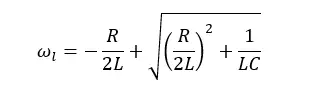
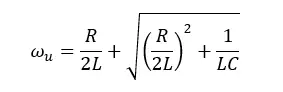
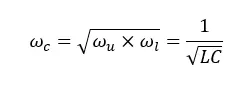
The quality factor (Q) of a band-pass filter can be defined as the ratio of the center frequency to the bandwidth.

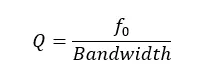
If the value of Q (quality factor) is higher, the bandwidth will become narrower. So that shows better selectivity for a given value of f_o. (Q>10) as a narrow band or (Q<10) as a wide band.