Viscoelastic Models for Polymers

Viscoelastic materials and Viscoelastic Models

Viscoelastic materials are materials that have both viscose and elastic properties. When energy is applied to a completely elastic (ideal elastic) material, the energy will be stored as potential energy. When the energy is released, the material will come to its original position using the stored energy. When the energy is applied to a complete viscose (ideal viscose) material, the supplied energy will dissipate as heat.

Polymers are viscoelastic materials. Therefore, when a polymer is applied energy, a part of the energy will be stored due to the elastic components and other parts of the energy will be dissipated as heat due to the viscose components.

Viscoelastic Models

Several models have been introduced to explain the viscose and elastic behavior of viscoelastic materials. Ideal viscose materials are described using dashpots and ideal elastic materials are described using springs. By combining dashpots and springs together, viscoelastic models have been developed. A good viscoelastic model should be able to explain creep, relaxation, and recovery using all the components (spring and dashpot) of the model.

Creep

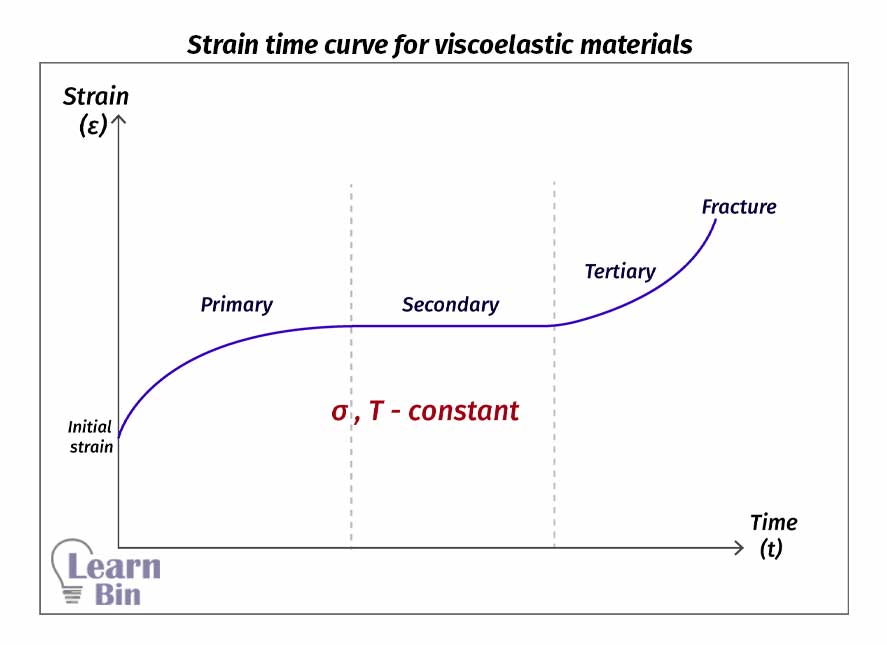
Creep is the strain that occurs as a function of time at constant stress. During the primary stage strain rate decreases with time. However overall strain will improve. Then it comes to the secondary phase. In the secondary phase, strain is constant. After a certain period, strain is improved rapidly and ruptured.

Stress relaxation

Stress relaxation is the decrease of stress at the constant strain. After the stress is removed, the stored energy on the elastic components is released. Due to the viscose components strain remains constant. If the material has more viscose components, it has high-stress relaxation.

Recovery

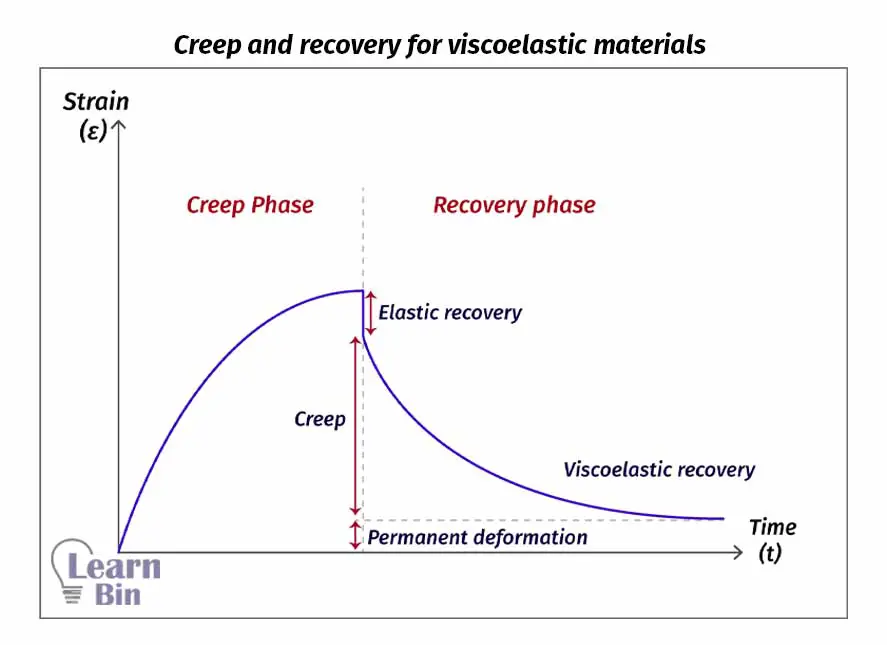
Recover is the process that the material comes back to its original state after the stress is removed.

Pure viscose and pure elastic models

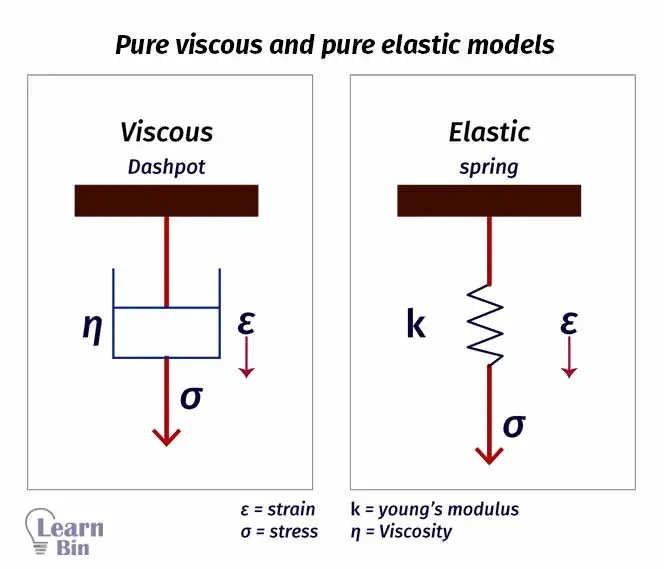
The behavior of pure viscose material and pure elastic material can be described using a dashpot and a spring respectively.

For the dashpot,

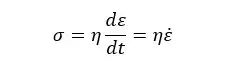
for the spring,

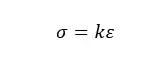
Where,

• σ = stress
• η = viscosity of the liquid
• ε̇ = strain rate
• k = Young’s modulus

Kelvin model

Kelvin model also known as the Voigt model is the simplest viscoelastic model. To describe the viscose and elastic components, a pure viscose dashpot and pure elastic spring is placed parallel to each other.

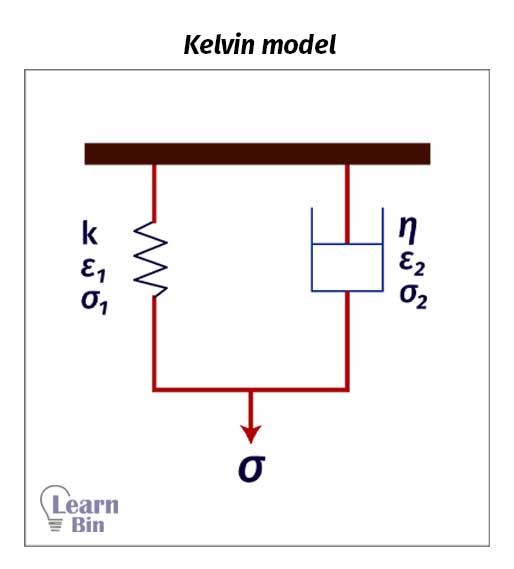
When applying stress both the spring and the dashpot undergo the same elongation. The total stress will be divided into spring and dashpot.

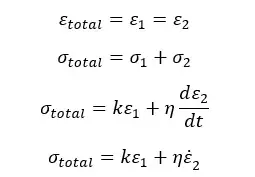
Energy is stored in spring. After the stress is released, only the spring will undergo relaxation. Dashpot is not involved in relaxation. Therefore, this model is not suitable for describing relaxation. But it is used to describe the creep.

Maxwell model

In the Maxwell model, a pure dashpot and pure spring are placed in the serial.

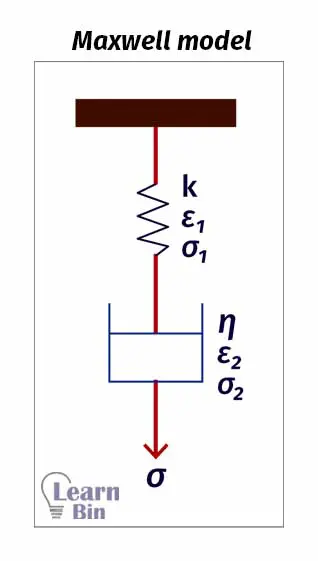
When applying stress, there will be a sudden deformation due to the sudden response of the spring. And there will be further strain due to the deformation of the dashpot.

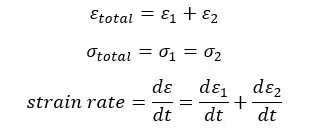
The strain rate of the spring,

• Where σ̇ is the stress rate.

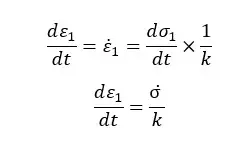
The strain rate of the dashpot,

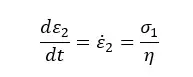
Therefore, the total strain is given by,

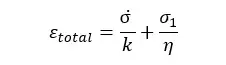
Once the force is removed, the spring will come to its original state. The dashpot will not recover. The deformation takes place of each component in the model separately. Deformation and recovery of the spring will not be affected by the dashpot. Therefore, the creep cannot be described by this model.

Burger model

The burger model is a combination of both the Maxwell and kelvin models. It describes the viscoelastic behavior (creep, relaxation, and recovery) of non-Newtonian fluids. In this model, the Kelvin unit is placed in between the Maxwell unit.

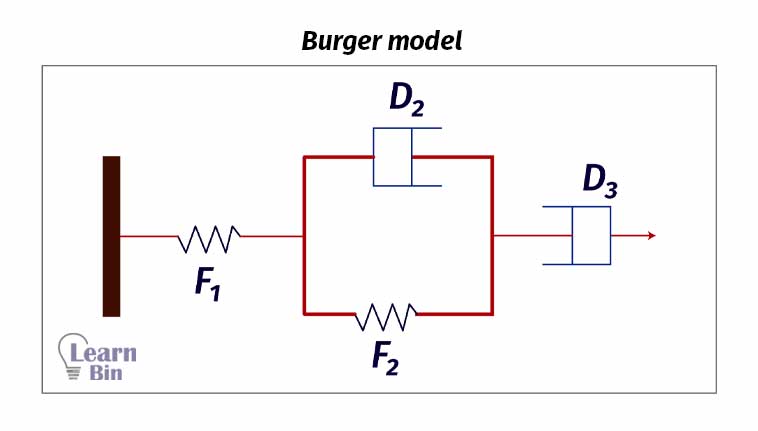
Once we apply stress, the F₁ spring will come to its maximum strain within a very short time. This explains the elastic domain of the materials. When we further improve the stress, F₂ and D₂ start to strain. This represents the viscoelastic behavior. as we improve the stress further D₃ dashpot starts deforming permanently. This shows the viscose behavior of the materials.

• ε₁ = Pure elastic strain (Spring F₁)
• ε₂ = Viscoelastic strain (Parallel connection of Spring F₂ and damper D₂)
• ε₃ = Pure viscous strain (Damper D₃)
• ε_max = Maximum strain (ε₁ + ε₂ + ε₃)
• ε_E = Elastic recovery (Spring F₁)
• ε_VE = Viscoelastic recovery (Spring F₂ and damper D₂)
• ε_V = Viscous deformation (Damper D₃)

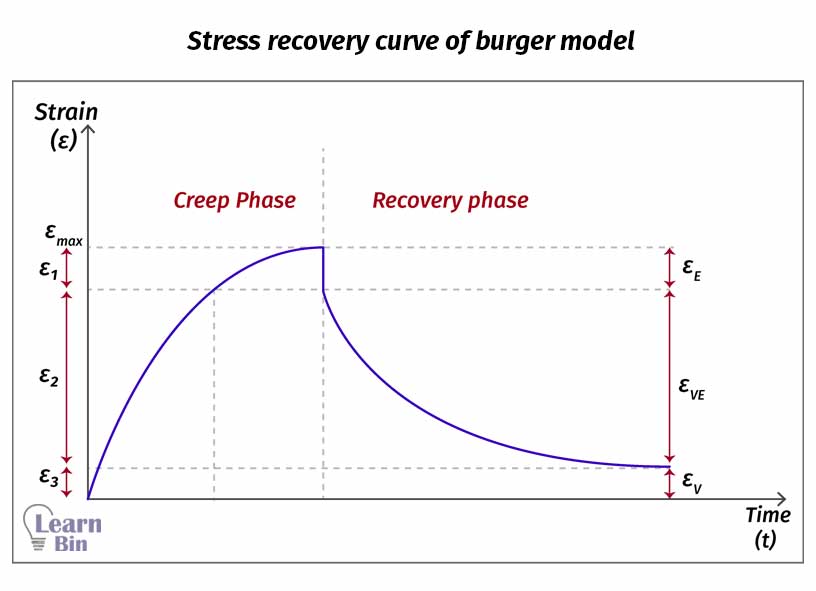
During the recovery process, the F₁ spring recovers suddenly. then there is a slow recovery from the middle Kelvin unit. Afterward, there is a permanent deformation due to the damper D₃.